A comment made on the previous post on the topic of hexa-coordinate carbon cited an article entitled “Observation of hypervalent CLi6 by Knudsen-effusion mass spectrometry“[cite]10.1038/355432a0[/cite] by Kudo as a amongst the earliest of evidence that such species can exist (in the gas phase). It was a spectacular vindication of the earlier theoretical prediction[cite]10.1021/ja00379a051[/cite],[cite]10.1021/ja00356a045[/cite] that such 6-coordinate species are stable with respect to dissociation to CLi4 and Li2.
The terminology describes these lithium carbides as effectively hypervalent; Kudo in the abstract of his 1992 article uses the more explicit phrase “carbon can expand its octet of electrons to form this relatively stable molecule“. We are taught early on in chemistry that the carbon octet is due to double occupation of four molecular orbitals formed using linear combinations derived from the relatively low energy 2s/2p carbon atomic orbital basis. Octet expansion on carbon must therefore involve to some degree the next atomic shell (3s/3p), which is normally regarded as too high in energy to be capable of significant population for carbon. But use of the 3s/3p shell seems at first sight inevitable. If one constructs an octahedral complex CLi6 surely ten electrons must be involved in bonding, four from the carbon and six from the equivalent lithiums? The 3s/3p carbon population must therefore be ~2 electrons, and we can truly describe a molecule where carbon has of necessity expanded its octet of electrons to ten as hypervalent. Or can we?
How does a quantitative (ωB97XD/6-311++G(d) ) calculation[cite]http://hdl.handle.net/10042/24790[/cite] reveal this effective hypervalency?
- The octahedral geometry is indeed a stable minimum, with the lowest vibrational wavenumber being 194 cm-1.
- It also checks out as clearly a closed shell species, stable to open shell perturbations.
- An NBO analysis reveals the Rydberg population (those 3s/3p atomic orbitals) to be only 0.09 electrons.
- It partitions the electrons into 13.97 for the 1s cores of the seven atoms, 7.67 “valence-Lewis” (i.e. shared covalent) and a mysterious 2.27 (valence, non-Lewis).
We now have a problem. One of the standard methods for partitioning electrons has isolated two of our ten electrons and placed them, with small partial occupancy, into unshared “lone pairs”, located as it happens on the lithium atoms (shown below for one of these partial lone “pairs”). The carbon is NOT hypervalent, and it has NOT expanded its octet.
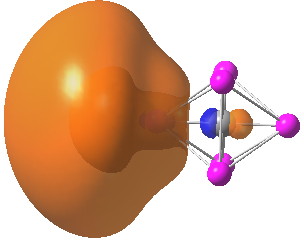
Click for 3D
So I tried another procedure, deliberately chosen to be rather different from the orbital-based NBO formalism. This is analysis of the ELF, or electron localisation function, and represents an attempt to derive the result based on a function related to the electron density. The red spheres shown below are the centroids of the twelve ELF basins located:
Click for 3D
Each of these (equivalent) basins has an electron population of ~0.81, making ~9.7 electrons in total. Each lithium sits on a square arrangement of four of these basins, and so has access to ~3.2 valence electrons. How do we interpret the situation for carbon however? Does its valence shell contain an expanded 9.7 electrons? Well, not necessarily. You can see that each of the basins has a three-centre relationship between the one carbon and TWO lithiums. These electrons contribute not just to C-Li bonding, but also to Li…Li bonding. So these 9.7 electrons contribute in part to bonding that does NOT involve the carbon. We can see this in the (Wiberg) bond orders, 0.254 for the C-Li interaction, and 0.116 for adjacent Li…Li interactions (such an explanation was also suggested for why II7 has no expanded octet at the central iodine). In fact, the origins of this effect were first clearly identified in the theoretical analysis of 1983[cite]10.1021/ja00356a045[/cite]: “the extra electrons beyond the usual octet are involved with metal-metal bonding rather than with interactions of the metals with the central atoms“.
It is nice to see that despite the passage of 30 years, and despite the introduction of many new ways of analysing the wavefunctions and hence the bonding of molecules, the essential original interpretation[cite]10.1021/ja00356a045[/cite] remains robustly correct!
Tags: energy, gas phase, Knudsen, low energy 2s/2p carbon, metal-metal bonding, pence
John Pople also would have appreciated your support of our 1983 interpretation. According to the 19th century definition, the valence of carbon in CLi6 is six (its “combining capacity” for six univalent Li’s). QTAIM fans will appreciate that CLi6, as well as its dication (which follows the octet rule) both have 6 bcp’s. Chad McKee in my group also has now found 6 bcp’s to the hexavalent central carbons in octahedral CAg6, CCu6, C(SiH3)6, and in the central CFe6 moiety of a nitrogenase model. Schmidbaur’s X-ray with a C(Au)6 moiety is another experimental example, as is Hogeveen’s dication, [C(CH3)6](2+) which has a hexavalent C with six C-C bonds (all with bcp’s)! There are many more computed examples of hexavalent (and >4 valent) carbons. Organic textbooks take note! These do not violate that octet rule, since fewer than two electrons are involved in each “bond.”
Thanks Paul. Yes, when I discuss eg PCl5 with my organic colleagues, octet expansion to 10 is more often than not mentioned. Yet, the alternative interpretation, that the Lewis “electron pair” is not sacrosanct, and that a bond can comprise eg 1.6 shared electrons is less often taught so it seems.
But as we know, a “bcp” does not necessarily constitute a valency, although we would all agree it probably constitutes a coordination. Thus many close H…H contacts also exhibit a bcp, but few of them would be called a “dihydrogen bond” (the exception might be eg H3N-BH3).
In another post, I noted a carborane where one of the boron atoms has 11 bond critical points associated with it. And I think that Xe2@C60 may have many more still.
In the above comment, I noted in passing that H3N-BH3 might have a bcp (bond critical point) between two hydrogen atoms that might genuinely indicate what a chemist would call a “bond”. Here I include a diagram of the QTAIM analysis for the extended crystal lattice of this species (itself determined by neutron diffraction).
The magenta arrow points to a 4-coordinated hydrogen, and the orange arrow to a 3-coordinated H. The green spheres represent the bcp coordinates, and in this case probably represent “dihydrogen” bonds (the red spheres are ring critical points).
Back in 1987 Jim Ritchie and I investigated a wide range of organolithium compounds using AIM (DOI: 10.1021/ja00254a004). For CLi6 we found the integrated charge on each Li is +0.73, making the charge on carbon -4.38. There are no bond paths between any of the Lithium pairs. We argued that there was no Li-Li bonding, rather the C-Li is primarily ionic, and that carbon can actually “have” more than 8 valence electrons by having some population in its 3s orbital, which is stabilized in the local electrostatic environment created by the octahedral arrangement of the 6 lithium cations. I would not call the carbon here hypervalent because the bonding is not covalent.
Steve,
For the 6-311++G(d) basis, the total Rydberg population is computed as only 0.09 electrons in the 3s/3p shell. I checked your impressive 1987 study, and it used the rather smaller 3-21G basis (does this define any Rydberg functions?).
It is also not entirely clear how we may relate a AIM bond path to “bonding”. There are many examples of a bond path being identified in ρ(r ) which is repulsive (as in cis-butene) and which a chemist would not call a bond (can one have repulsive bonds?) and conversely the lack of a bond path for situations where a chemist would indeed describe a bond (as is the case with the cycloheptatrienyl cation, the famous homo-aromatic system, where the homo-bond is also described as the “no-bond bond”).
There is other strange behaviour. For example in a classical alkene π-complex, one might have an identified bond path not between two nuclear attractors (the normal definition of a bond) but between one nuclear attractor and one bond critical point. This is kind of like the valley-ridge inflexion points in potential energy surface. Is a path between a nucleus and the mid point of a bond also a bond? These sorts of behaviours arise from a phenomenon known as annihilation, whereby a bond critical point (and hence its path) can be annihilated by an adjacent ring critical point (which the Poincare-Hopf theorem allows). In these examples, the topology is said to be “unstable”.
Then there are the “non-nuclear attractors”, ie regions which resemble a nuclear attractor in their topology, but for which no nucleus actually exists. The famous example of this is H3+ which has only bond paths between the three hydrogens and the non-nuclear attractor at the centroid, but no actual H…H bond paths.
These sorts of issues illustrate why QTAIM polarised often into two camps, which might be reduced/simplified to the physicists vs the chemists, and why “bonds” continue to be difficult to pin down beyond all dispute.
I conclude this rather lengthy reply by citing I.I7 (an analogue of IF7) which I posted upon a little while ago where the central iodine does not expand its octet valence shell (although most chemists would intuit that it does), and the six extra valence electrons all occupy the I…I regions (as a prelude to reductive elimination of I2). This might be regarded as an extreme example of CLi6. I notice from that post that I did not include a QTAIM analysis; I will chase it up to see what that looks like. Oh, I selected I.I7 precisely to reduce the ionic character and promote covalent character.
I noted in the previous comment some characteristics of QTAIM analysis, and in particular mentioned II7. Shown below is a QTAIM analysis of this system. The green spheres are bond critical points. The pertinent features are the bcps between each radial iodine and the central one (ρ(r ) 0.046) and the peripheral ones (ρ(r ) 0.018). The latter illustrate the I…I interactions. Most significant however are the two critical points highlighted with a magenta arrow. The green one is a bcp, the smaller red dot a rcp. Notice that they are relatively close together. Indeed, any closer and they would self-annihilate. The I…I bond path would vanish.
I would assert that for eg CLi6 exactly this annihilation has occurred, and that this is the reason for no Li…Li bond path. Or to put it another way, depending on the geometry and topology, bcp+rcp annihilation may or may not occur. A physicist would therefore assert that bonds can be annihilated. A chemist might be tempted to say that other metrics of a bond, such as eg a bond order index, are better representations of “chemistry”.
[…] in some way with the central atom. An expanded octet in other words. Well, if you take a look at earlier blogs, you may have observed that this expanded octet is not real (IMHO). If it’s not real, then we […]