A little while ago, I set out some interpretations of how to push curly arrows. I also appreciate that some theoretically oriented colleagues regard the technique as neither useful nor in the least rigorous, whereas towards the other extreme many synthetically minded chemists view the ability to push a reasonable set of arrows for a proposed mechanism as of itself constituting evidence in its favour.[cite]10.1186/1752-153X-7-94[/cite] Like any language for expressing ideas, the tool needs a grammar (rules) and a vocabulary, and perhaps also an ability to carry ambiguity. These thoughts surfaced again via a question asked of me by a student: “is the mechanism for the hydrogens in protonated benzene whizzing around the ring a [1,2] or a [1,6] pericyclic sigmatropic shift?”.
I must first explain the “rules” I used to produce the diagram above.
- An arrow comprises an (approximate) electron pair (in the Lewis sense)
- And it operates on individual resonance/valence bond representations
- A sigmatropic shift is a pericyclic reaction, and one should be able to construct arrows which both conjugate in a cyclic sense, and
- can be represented in either a clockwise or anticlockwise cyclic direction.
- As a thermally allowed pericyclic reaction, we will endeavour to use only 4n+2 electrons in our arrow pushing (an aromatic transition state for the process). For this molecule, it means either 2 or 6 electrons (one or three arrows, again in a Lewis sense)
- I also use the convention in which the origin of an arrow is the midpoint of a (covalent) bond, and its destination the midpoint of a forming (covalent) bond, represented above by a dashed line. Here, I am guided by the observation that the “coordinates” of the start and the end-point of such arrows can be obtained by QTAIM theory, which provides them via so-called “bond critical points“.
So for the 2-electron/one arrow process, we should be able to come up with two schemes, one clockwise, one anticlockwise. It is really easy to show one of these (rhs for [1,2]), but it is a true head-scratching time to produce the other. I have done so via the red arrow in representation 1 above. More of this in a moment.
For the 6-electron/3-arrow alternative, we start with three distinct resonance/valence bond forms for the pentadienyl cation, and each of these again should manifest as arrows drawn in both clock directions. Five cause no problems, but the sixth again carries a very odd arrow (red, representation 2 above).
What does that red arrow mean? Dissected into smaller steps, it consists of two arrows, joined head to tail in a daisy chain, but still clearly counting as just a single electron pair. The first component of this portmanteau arrow represents the formation of benzene and a proton, the geometry of which in fact resembles the formation of a π-complex between the two. The second component represents the breakdown of this complex to reform a classical carbocation. The daisy-chained arrow passes through the middle of a single bond, which achieves the necessary cyclic conjugation, and then continues on its way to a final destination at the mid-point (approximately) of a C-H bond. If it is drawn as a simple arrow (avoiding passage through the single bond), the mechanism “does not work”; the wrong carbon gets connected to the shifting hydrogen.
So this little thought experiment has produced a new entry in the arrow-pushing vocabulary; a daisy-chained arrow, and a new rule which requires it to pass through (interact with) a bond, but without stopping. To ask if this invention has any connection to reality, its time for a full-blown quantum mechanical computation of that transition state (an IRC for which[cite]10.6084/m9.figshare.717183[/cite] is shown below).

If you look very carefully at how the representation of the magenta-coloured bond (scheme above) changes during the IRC, you will note that at the transition state it is shorter (1.439Å) than at the start or the end (1.462Å). The magenta-bond order at the transition state is 1.17 (Wiberg), and the bond is clearly “involved” in the process. This does hint that the representation 1 or 2 in the scheme above may be making a significant contribution. None of the other forms of arrow pushing in that scheme involve any arrows either starting or ending at that bond, so they cannot account for the change in bond length/bond order of that bond. We interpret the daisy-chained arrow as carrying more information than a normal arrow would regarding the timing of the process; the path up to the transition state is represented by the first part of the double-headed arrow, and the path down to the product by the second component of that arrow. So up to the first arrow-head, electrons are moving towards the magenta bond, and in the second phase, they continue their journey by moving onwards and away from that bond.
Is there any prior art (precedent) for such a process? We actually, there is a very nice example; the dyotropic rearrangement of a 1,2-dibromoethane (which was recently experimentally shown to be a concerted process with double inversion of configuration at the carbon bearing the bromine[cite]10.1039/C2CC33676F[/cite]). That too involves a transition state where the central C-C bond is shorter (1.41Å) than either reactant or product (1.50Å)[cite]10.1002/chem.200501517[/cite]. We may represent the arrows involved in the process in two ways in a manner analogous to structure 1 above, but this time involving two daisy-chained arrows (red and blue below). This does not necessarily imply that at the transition state a full triple bond has formed, merely that as the arrow “passes through the bond” its bond-order temporarily increases. The conventional arrow pushing on the right implies no change whatsoever in that central bond. Like any set of (non-equivalent) resonance representations, these two sets of arrows taken together may be a more realistic one than either individually for the overall reaction.
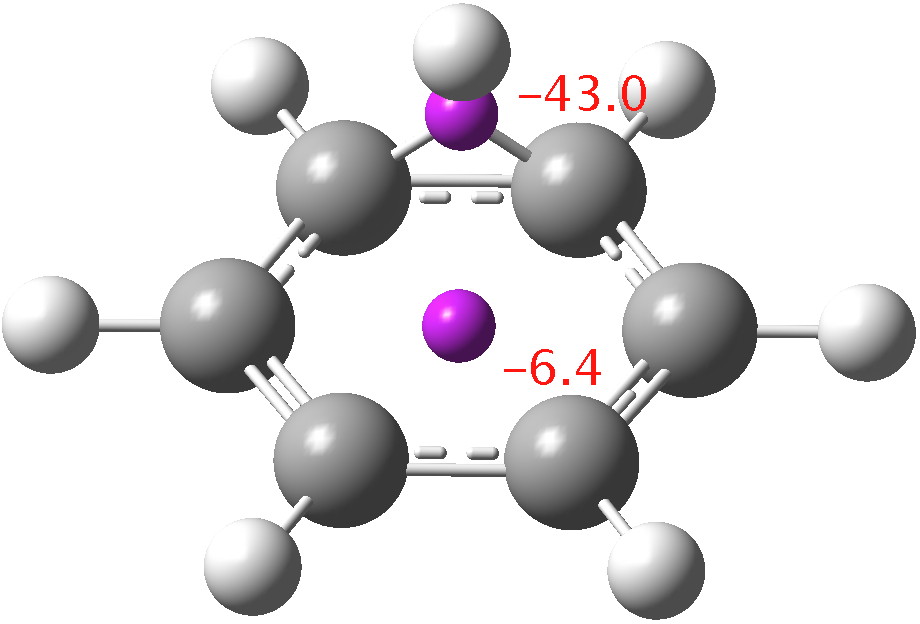
I conclude with some thoughts about another question: is the process a [1,2] or a [1,6] sigmatropic pericyclic reaction? If you regard pericyclic reactions as manifestations of aromatic transition states, you could equally well ask; given a choice, does a system prefer 2-electron or 6-electron aromaticity (both of course conform to a 4n+2 rule). To try to cast light on that, I show the computed NICS values at two points (magenta spheres), the first being the RCP (ring critical point in a QTAIM analysis of the transition state) of the 6-ring and the second the BCP of the 3-ring. If we calibrate this to -10 ppm (for benzene itself), the 6-ring is seen to be only modestly aromatic on this scale. The 3-ring (corresponding to 2-electron aromaticity) appears to be highly aromatic, but this is probably due to a large contribution from local shielding effects; NICS for small rings is not reliable. But this does constitute a hint that, all other aspects being equal, 2-electron aromaticity may have the edge over 6-electron aromaticity. Clearly more work is needed on this aspect.
Whether or not you believe in the theoretical rigour of arrow pushing (or indeed its absence of rigour), I would suggest that it has proved a useful tool, a mechanism if you like, for helping to think about how reactions proceed. Certainly I also consider it desirable, if arrow pushing is to continue as a useful tool up to its 100th birthday, that some effort should be devoted to updating it for 21st century chemistry.
[cite]http://hdl.handle.net/10042/24720[/cite]
Tags: first arrow-head, Reaction Mechanism, Tutorial material
Some thoughts on that:
1. Inspired by Ivar Ugi’s “principle of minimum chemical distance” one would be tempted to assume that 1,2 is the “correct” answer.
2. I have calculated the magnetically induced currents in the TS state, they are dominated by far by the typical field you have in benzene (see the wikipedia article on Aromatic ring currents), also the total induced molecular current is virtually the same as in benzene, but then you have also a minute diatropic loop going around the wandering proton. I have not managed to integrate to little current loop yet, but I could well be that it compares well with a diatropic current you expect from a 1,2.
3. Maybe they do not have to be mutual exclusive!
4. To me the questions seems the other way round then what should be asked. Chemical models usually do not neccessarily claim any reality per-se. Muchmore you use a simple model to predict what happens in reality. Many “controverses” in computational chemistry arise from such an assumption of a model having a correspondence in reality. One of my favourite examples is the good old ligand field theory which is a gem of predictive power. But then its common sense in theoretical chemisty, that it is based on wrong assumptions, hence its wrong per-se. Nevertheless everyone uses it including the theoreticians who know that it is “wrong”.
Re: “principle of minimum chemical distance”. The reverse is sometimes called “non-least motion pathways”. I think in pericyclic reactions where orbital symmetry plays a role, one has many examples of such reactions taking “the long way round”. And when dynamics is factored in, one sees examples where the most probable pathway is not the one passing through the lowest energy point on the potential. So this question of [1,2] vs [1,6] could be expressed as “rearrange the minimum number of electrons”. But an answer that involves BOTH pathways is interesting as well.
Re 4. I think the question could be posed as “is arrow pushing a model which can be used to make predictions?” In this example, and also the dyotropic system, application of the model seems to predict a “non-least motion” behaviour at the central C-C bond, which contracts in length and then expands again. Of course that itself is merely the behaviour of a “high level” calculation and is not actually an experimental measurement.
But another question might be: “is arrow pushing theoretically unsound”. I do not believe it is wrong as such, merely a simplification. But some could argue it is too gross a simplification. My argument here in part was that if arrow pushing is applied to eg a dyotropic, it seems to capture quite subtle behaviour which might not be expected of an over-simplified model.
Re “3. Maybe they do not have to be mutual exclusive!”. Below is an example of a simple, apparently 6-electron electrocyclic ring opening that could use either of its two sets of six electrons. In fact, BOTH seem to happen concurrently; at the transition state, the NICS values at the centroids of both rings are -12 ppm (a typical aromatic transition state with strong diatropic ring currents). This value is about twice that of the NICS for the [1,6] shift, which is why I queried it. But its low value might simply reflect inappropriate use of NICS!
[…] I have noted elsewhere, the curly-arrow representation of reaction mechanism has hardly evolved over the last sixty years. […]
[…] It also has the feature associated with dyotropic rearrangements[4] that the central S-S bond is shorter at the transition state ((1.937Å) than for either reactant or product […]
I think for answering the type of pericyclic sigmatropic shift 1,2 or 1,6, we have to consider some figures from FMO and the basic rule of this kind of reactions (Supra-Supra, Supra-Antra and ….). my question is about structure 1, if we consider 1,2 shift what is the meaning of red arrow to middle of carbon-carbon bond based on FMO or W-H rules (is it forbidden or allowed)? another question is that, is it possible for proton to migrate from one side to another side of benzene ring via sigma complex?