I occasionally delve into the past I try to understand how we got to our present understanding of chemistry. Thus curly arrow mechanistic notation can be traced back to around 1924, with style that bifurcated into two common types used nowadays (on which I have commented and about which further historical light at the end of this post). Here I try to combine these themes with some analysis of wavefunctions for a particularly troublesome reaction to represent, the dibromination of an alkene, which I represented in the previous post as shown below.
However, that first step in the mechanism (red box above) has been represented in two other ways in the past. The green box used to be common, but is now being superseded by the magenta style (as for example here).
I should first explain (what I think is) the intent of these three schemes (this is not really declared very formally, and so I am interpreting rather than stating):
- The green scheme, showing two arrows, attempts to illustrate a nucleophile (the alkene pπ electrons) interacting with an electrophilic acceptor (the Br-Br σ* bond) in a filled/empty orbital sense.
- The magenta scheme, showing three arrows, adopts a notation where a nucleophilic electron pair attacks an electrophilic atom centre to form a new bond between the two atoms.
- The red scheme has the nucleophilic electron pair terminating at the (approximate) bond centroid of the newly forming bond rather than at the atom.†
I set out to see what light quantum mechanics might be able to cast. To do so, I subjected the wavefunction of the system shown in the blue box above to analysis, which represents the species being formed as a result of the curly arrows pushed in the schemes above.
Firstly, QTAIM, which determines the topology of the electron density in the molecule. The green dots in this diagram are what are called “bond-critical-points”, or BCPs. The numerical values associated with each green dot are the electron density ρ(r) at that point.
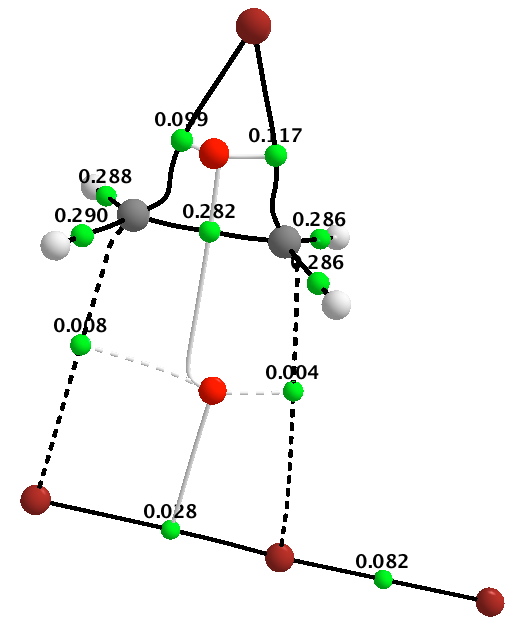 Now, I have pointed out elsewhere that the existence of such a topological feature does not necessarily coincide with what we think of as a bond. With that caveat in mind, one can see that the BCPs reveal a cyclobromonium ring, with one C-C single bond (from the value of ρ(r) ), two C-Br bonds, and a ring point (shown in red). The slightly weaker bond (again from the value of ρ(r) ) is the one about to cleave as a result of the tribromide anion attacking the carbon, with inversion of configuration at that carbon.
Now, I have pointed out elsewhere that the existence of such a topological feature does not necessarily coincide with what we think of as a bond. With that caveat in mind, one can see that the BCPs reveal a cyclobromonium ring, with one C-C single bond (from the value of ρ(r) ), two C-Br bonds, and a ring point (shown in red). The slightly weaker bond (again from the value of ρ(r) ) is the one about to cleave as a result of the tribromide anion attacking the carbon, with inversion of configuration at that carbon.
This picture does seem to correspond to our intuitive thoughts about mechanism. It offers a way of interpreting the arrow pushing scheme shown in red above. In this sense, an arrow would start at a BCP of a nucleophilic (donor) bond in the reactant, and terminate at the BCP of the acceptor bond formed in the product. Should we need to do so, we could derive precise 3D coordinates of the relevant BCPs, and ensure that our curly arrows either start or end precisely at those coordinates. This method would not allow for example the magenta scheme, since the terminating point of what is after all an electron arrow cannot be at a nucleus but needs to be at a bond (critical point). There is however one aspect un-answered. Both the red and magenta schemes have one arrow starting at an electron “lone pair”, and QTAIM does not give us coordinates for these! I will deal with this aspect last.
Yet another way of looking at it is to interpret the wavefunction in terms of pairs of (doubly) occupied and empty localised orbitals so that a donor-acceptor interaction energy can be derived. On to the NBO technique (natural bond orbitals), which tells us about the donor/acceptor interactions within a molecule. This relates to how the green box above might be viewed. When this is done, two sets of NBO orbital pairs are especially pertinent; each is a (doubly occupied) donor originating from the alkene (purple and orange) and an (empty) acceptor corresponding to the Br-Br cleaving bond (red and blue). In the overlay of two NBOs below, the purple (donor) and blue (acceptor) densities are overlapping in-phase to form a C-Br bond (arrow 1) Equally, overlap of an orange (donor) originating in part from a lone pair on bromine and the red acceptor (from the B-Br anti-bond) are forming the second C-Br bond (arrow 2). This actually corresponds more closely to the magenta than the green box.
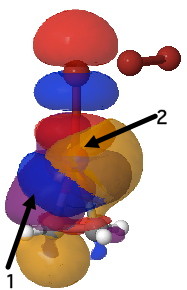 NBO Analysis. Click for 3D. |
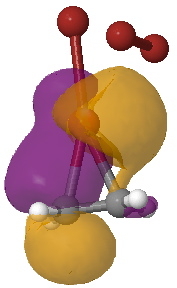 NBO Analysis. Click for 3D. |
This brings us back to a deficiency of QTAIM; it does not tell us what kind of bonds we are dealing with. We might have presumed that the formed C-Br bonds of the bromonium ring (e.g. blue box) were single and hence two-electron bonds.
We have one more way of looking at bonds, and this method also allows us to count the electrons in the bond. Remember, a bond does not have to contain integer numbers of electrons! It can just as easily be fractional, as for example in PF5. ELF (the electron localisation function) is a way of looking at the properties of the electron density to identify localised spin-paired probabilities. The ELF technique partitions the function into discrete basins, and these can then be integrated for the total number of electrons defined by the ρ(r), the electron density. The centroids of these basins then give us something actually quite similar to the bond-critical-points from QTAIM theory, but carry two additional benefits. Firstly, the total electron count associated with each basin. Secondly, it also gives us the centroids of any lone pairs (which we identified as something helpful for defining either a start point or an end point of a curly arrow in arrow pushing). I show below the ELF analysis of the ion-pair intermediate of this bromination (i.e.the outcome of the arrow pushing in the red or magenta boxes). The red dots are basin centroids; there are lots of them but I concentrate only on the two marked with black arrows. They are the result of the donor-acceptor orbital overlaps, the principle one of which was shown above. These two ELF basins each have electron integrations of ~1e. Each C-Br “bond” contains only one shared (i.e. covalent) electron.
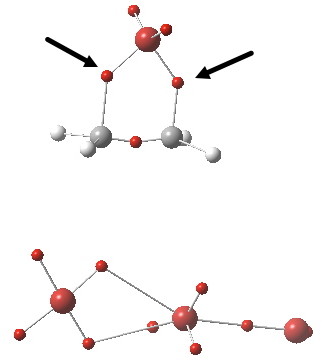
Click for 3D.
So which of the three schemes above is the most realistic? Well, the green scheme uses only one curly arrow in the carbon-bromine region, and so it carries the message that the bonds in this region only involve two electrons. The red scheme corresponds closely to the topology of the electron density involved in the reaction, but clearly, its arrows are NOT simple two-electron arrows. Neither are those of the magenta scheme, which seems rather to fall between two stools; it is not accurate topologically, but neither are its arrows simple two-electron arrows.
My conclusion must be a reminder that when we push curly arrows, we may not necessarily be able to associate these arrows with simple pairs of electrons. This is quite a subversive statement to make. But then again,surely the concept of curly arrow pushing, dating as it does from 1924, is overdue a makeover?
† Alan Dronsfield has contacted me with some information about when styles 2 and 3 might have bifurcated. Two particularly influential early text-books on mechanism, one published by Gould in 1959 and another by Sykes in 1961, appear to have adopted respectively the magenta and red schemes.
Tags: Alan Dronsfield, donor-acceptor interaction energy, Gould, Reaction Mechanism, Tutorial material