Two years ago, I discussed how curly arrow pushing is taught, presenting four different ways of showing the arrows. One of the comments posted to that blog suggested that all of the schemes shown below were deficient in one aspect.
The issues were the stereo and regiochemistry. In particular, the diagram above carries no explicit information about the symmetry of the electrons from which the first arrow originates; it is considered only implicit that we are referring to the π-electrons of the alkene, and that this in turn imparts stereochemical information which is absent from the diagram itself. This deficiency can indeed be traced back to the first ever representation of curly arrows, where the distinction between π- and σ-electrons was not made, and which in that example can cause much confusion about the properties of the molecule being considered. It is in some respects surprising that a notation first proposed in 1924, in effect before quantum mechanics as applied to chemistry had properly matured, is still largely intact and unchanged since that day.
Are curly arrows ripe for reform? In order to try to move this debate forward, I decided to investigate precisely the reaction shown above using quantum mechanics (ωb97xd/6-311g(d,p)/scrf(cpcm=water) The results will be presented as an intrinsic reaction coordinate of the precise reaction shown above. Before revealing it however, I should note that the scheme above in fact attempts to represent only part of a reaction; the formation of a carbocation by reacting propene with HBr. It does not reveal the end-game so to speak, in which the carbocation then reacts with the bromide anion to form 2-bromopropane. What is implied by the scheme above is that the propyl cation and bromide anion together constitute a discrete intermediate on the way to form this product, and that the overall reaction therefore comprises two discrete transition states and one intermediate; a stepwise reaction.
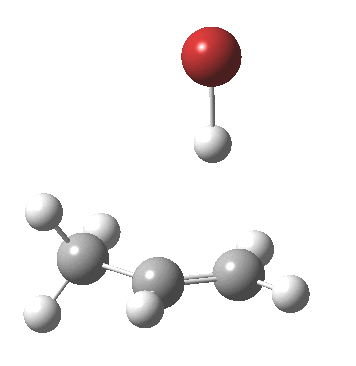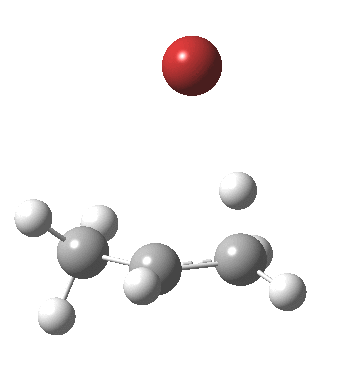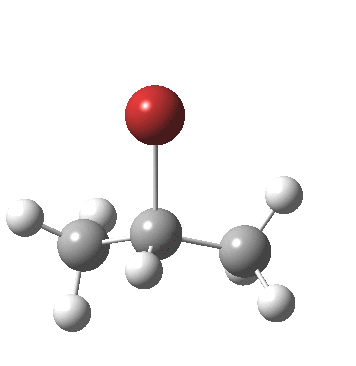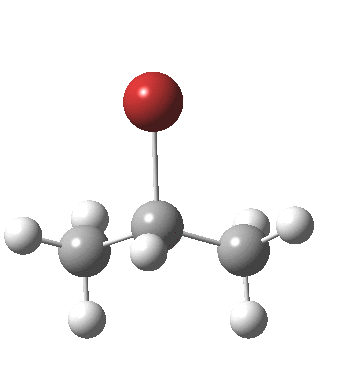
- The (optimised) geometry of the starting point (IRC = 3.5) is a hydrogen bonded complex between the alkene and the H-Br, interacting via the π-cloud of the former. This structure is offset from the mid-point of the double bond towards the less substituted end. We are here seeing Markovnikov’s rule in action.
- As a result, the proton transfer (IRC = 0.0) when it starts to happen, heads off for the terminal carbon rather than the middle one.
- After this point, note carefully that no intermediate carbocation/bromide anion pair is actually formed. Instead at about IRC -1.0, the bromide atom starts to move towards the central carbon to form a C-Br bond (IRC -2). The immediate outcome of this is that the newly formed C-Br and C-H bonds are conformationally eclipsed.
- At IRC -4, the final stage in the reaction starts to take place, a subtle rotation about the BrC-CH bond to remove its eclipsing nature.
If you compare this more quantitative scenario with that depicted in the original scheme at the top, you will notice that it does not capture the timing of any of the events described above and even appears to be quantitatively wrong in showing a carbocationic intermediate. This last aspect perhaps is because a curly arrow diagram does not attempt to describe the environment in which a reaction might find itself, which in this case may be an explicit hydrogen bonding solvent or Lewis acid catalyst. Thus the bromide anion may be stabilised by other species present in solution, perhaps to the extent of even forming an ion pair.
The point to take home from this however is that perhaps the next evolution of (schematic) curly arrows might be towards more quantitative reaction coordinate diagrams, expressed (as here) as an animated IRC. Indeed, I am (slowly) assembling a library of these for some of the more common reactions to be found in organic chemistry. And we should not forget that even these are defined by the model we construct, which may not include all of the components and conditions actually present when the reactions occur in reality.
Tags: deficiency, intrinsic reaction coordinate, Reaction Mechanism, Tutorial material

Very instructive animation and discussion, Henry! I note that a “least motion” cis addition pathway wins out, but without any indication of the “trans addition” we teach our students. How does this occur?
In that context I wonder about
(1) HBr addition to norbornene, where such “direct addition” completes with rearrangement-addition
(2) trans Br2 addition to ethylene in solvents like CCl4 is known. A bromonium ion may form, but how does the second Br get to the other side under such non-ionizing conditions?
The trans addition almost certainly requires a different model; perhaps involving two HBr units, one on each side of the alkene, and possibly a proton transfer chain to avoid the dipole moment building up to too large a value if the solvent permits.
Many reactions indeed require a lot of movement with one component “getting to the other side” and I think we need to think about models that can achieve this.
I have studied such non-least motion mechanisms for quite different reactions. An early attempt to do this for the E2 elimination appeared in this post, where both syn and anti modes were studied, and this involved adding a second halide anion to the model. The same approach was used to try to find out the balance between a ring migration reaction and an E2 elimination. The relative energies of the two modes certainly favours the anti elimination. However, I am not satisfied that either of these models is yet complete, since the overall charge on the model is -1 (coming from the second halogen). I feel the model will only be complete when the system is overall neutral, and an appropriate charge-balancing cation is somehow added.
Ian Fleming is famous (amongst other things) for his book “Molecular orbitals and Organic Reactions”. A colleague of mine (thanks James!) suggested that another way of regarding curly arrow pushing is to think of the arrows as reminding (perhaps representing is too strong a way of putting it) us of the underlying orbital basis of reactions. In this scenario we think of a curly arrow as representing the interaction of a filled orbital with an empty one, very much in the manner of the Klopman-Salem perturbation expression. Rather loosely, the origin of the arrow would be the filled (donor) orbital and its destination the region of maximum overlap between it and the empty (acceptor, and probably antibonding) orbital. The arrow in this interpretation can represent the formation of a new bond by the overlap of these two orbitals, and also the cleavage of the antibonding region. I have tried to represent these concepts here for the example described above.