The Baldwin rules for ring closure follow the earlier ones by Bürgi and Dunitz in stating the preferred angles of nucleophilic (and electrophilic) attack in bond forming reactions, and are as famous for the interest in their exceptions as for their adherence. Both sets of rules fundamentally explore the geometry of the transition states involved in the reaction, as reflected in the activation free energies. Previous posts exploring the transition states for well-known reactions have revealed that the 4th dimension (the timing of the bond formations/breakings) can often spring surprises. So this post will explore a typical Baldwin ring formation in the same way.
If you study the consequence of the mechanistic arrows shown above, you will see that the immediate product of the cyclisation is an internal ion-pair, a zwitterion. To get a realistic transition state geometry for a reaction where reaction of a neutral molecule creates charge separation, we need to build a slightly more elaborate system. The quantum mechanical model will include a continuum solvent (ωB97XD/6-311G(d,p)/SCRF=water) and because hydrogen bonds to charged donors or acceptors are often 2-3 times stronger than neutral ones, we need to include explicit solvent as well, as below.
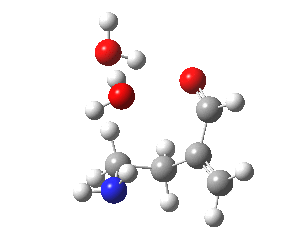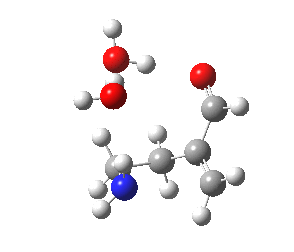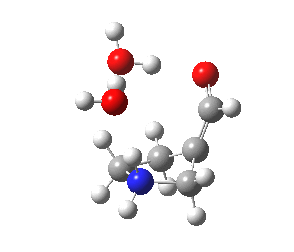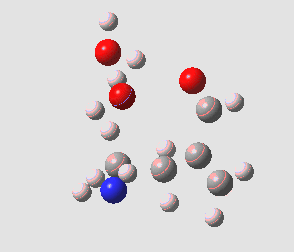
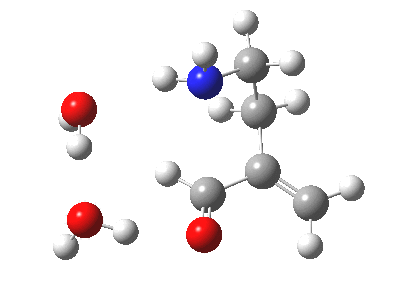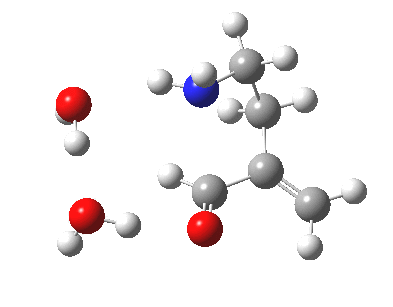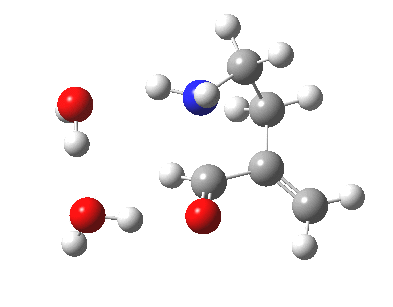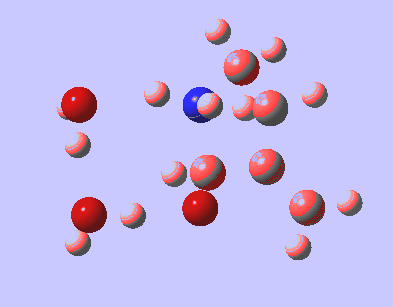
This resembles the strategy used for studying the Baeyer-Villiger reaction I showed previously, and also permits the system to transfer protons as appropriate. The 5-endo-trig transition state does indeed have such strong hydrogen bonds across the solvent bridge connecting the ionic centres. The angle of attack N-C-C is 92°. The IRC shows a barrier, which as ΔG is 17.8 kcal/mol.
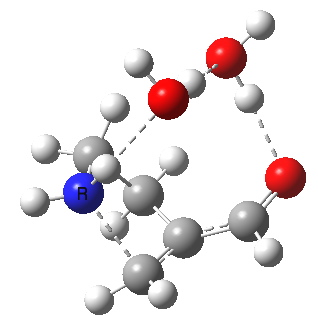 5-endo transition state. Click for 4D. |
 |
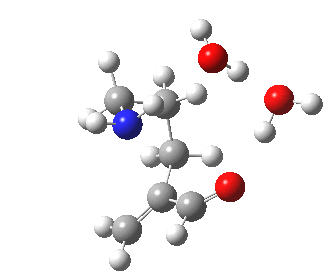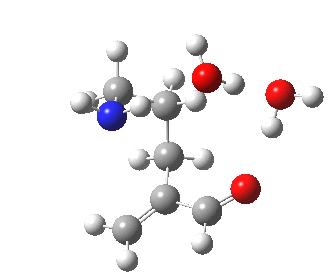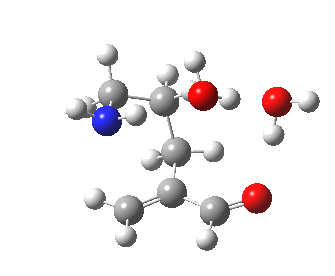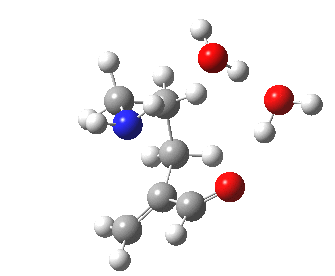
The 6-endo transition state, according to Baldwin, makes the transition from unfavourable to favourable, since the angle of attack by the (nitrogen) nucleophile on the double bond can now adopt the more favourable angle of 101° (although rather less than the conventionally assumed angles of 106-109°), and ΔG is reduced to 12.4 kcal/mol, a reduction of 5.4 kcal/mol over the 5-endo analogue, more than enough to turn a dis-allowed into an allowed reaction! The transition state adopts a beautiful chair-like shape.
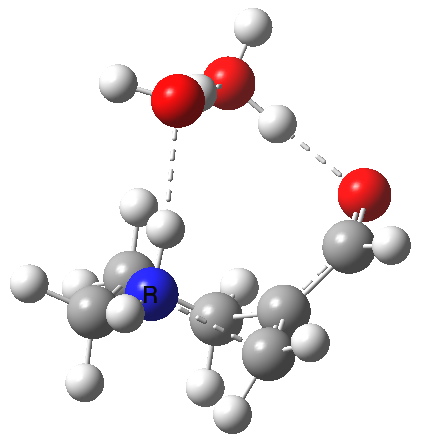 6-endo transition state. Click for 4D |
 |
To complete the comparisons, the 5-exo transition state and its IRC is shown below, revealing again a very strong network of hydrogen bonds connecting the zwitterion. The angle of attack is 112°, quite different from (and more favourable than) the 5-endo isomer, as is the (much lower) free energy barrier of ΔG 5.7 kcal/mol. It is worth noting that this transition state does not exist on the potential energy surface computed without the inclusion of two solvent molecules!
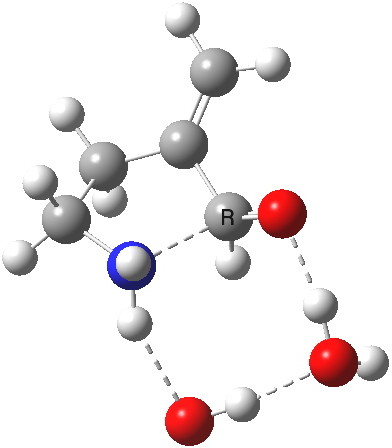 5-exo transition state. Click for 4D |
|
Because Baldwin’s rules are in fact a generalisation of transition state geometry, one might expect that the specific nature of each transition state must be considered, and that exceptions therefore could easily be contrived. What I wanted to show here is that constructing a realistic transition state for any specific reaction is in fact nowadays not that much more onerous than applying the rule! For a few hours more effort, one can have a much better analysis of any specific system.
Tags: Baldwins rules, free energy barrier, immediate product, potential energy surface, Reaction Mechanism, Tutorial material
[…] Henry Rzepa Chemistry with a twist « Transition state models for Baldwin’s rules of ring closure. […]
[…] Transition state models for Baldwin’s rules of ring closure. […]
Can I have the coordinates of the transition state?
All coordinates are available via hyperlinks to the FAIR data repository.