During the 1960s, a holy grail of synthetic chemists was to devise an efficient route to steroids. R. B. Woodward was one the chemists who undertook this challenge, starting from compounds known as dienones (e.g. 1) and their mysterious conversion to phenols (e.g. 2 or 3) under acidic conditions. This was also the golden era of mechanistic exploration, which coupled with an abundance of radioactive isotopes from the war effort had ignited the great dienone-phenol debates of that time (now largely forgotten). In a classic recording from the late 1970s, Woodward muses how chemistry had changed since he started in the early 1940s. In particular he notes how crystallography had revolutionised the reliability and speed of molecular structure determination. Here I speculate what he might have made of modern computational chemistry, and in particular whether it might cast new light on those mechanistic controversies of the past.
Charting the mechanistic pathway connecting 1 and 2 was first done by Capsi[1] using 14C labels (* in the diagram above, on a steroid derivative), when after claimed selective Birch reduction of the blue double bond in 2, alkene ozonolysis and decarboxylative loss of *, all the radioactivity ended up in the CO2. This showed[2] that the mechanism involved path (a). For paths (b) or (c), the label would have ended up at * and hence not oxidatively lost as CO2. Futaki[3] did the experiment in a different way, putting his 14C label in the position * where he found that only about half of the label was retained in this position (and then lost when he specifically degraded 2 by oxidatively removing that carbon). This now strongly implicated path (b), and also seemed to disprove not only path (a) but also mechanism (c), where a [1,5] shift should have retained the label at the original position (and caused all of it to be lost upon decarboxylation). It was these two apparently contradictory results that helped ignite the controversies.
All the routes (a)-(e) above involve pericyclic sigmatropic reactions, the understanding of which was about to be revolutionised by Woodward (with Hoffmann) in the mid 1960s. In fact, the mechanism here comprises a mixture of [1,2] cationic sigmatropic migrations and [1,5] neutral sigmatropic migrations. To balance one against the other, can computational chemistry come to the rescue? I first note that the mechanisms above are all shown as cations. Until recently, a computational chemist would simply set the charge on their model to +1 and proceed onwards and upwards. But now we can do a bit better. We can (arguably we always should) include the counterion, and so in my own exploration, I have included a perchlorate anion, and the whole study then becomes one of a neutral system (charge =0), a zwitterion. A B3LYP/6-311G(d,p) model with SCRF=water continuum solvent was employed. Let us see what emerges:
- Path (a) involves a [1,2] angular methyl (R=Me) migration, which turns out to have ΔG†28.5 kcal/mol. The IRC for this migration is shown below.
The (Wheland) intermediate then loses a proton to give 2.
- Path (b) involves an alternative rate-limiting migration of the angular methyl, ΔG† 30.2 kcal/mol, followed by two lower energy [1,2] migrations of the ring ΔG† 27.8 and 25.3, via a spiro-ring Wheland intermediate (relative energy +3.8 kcal/mol), and deprotonation to again give 2.
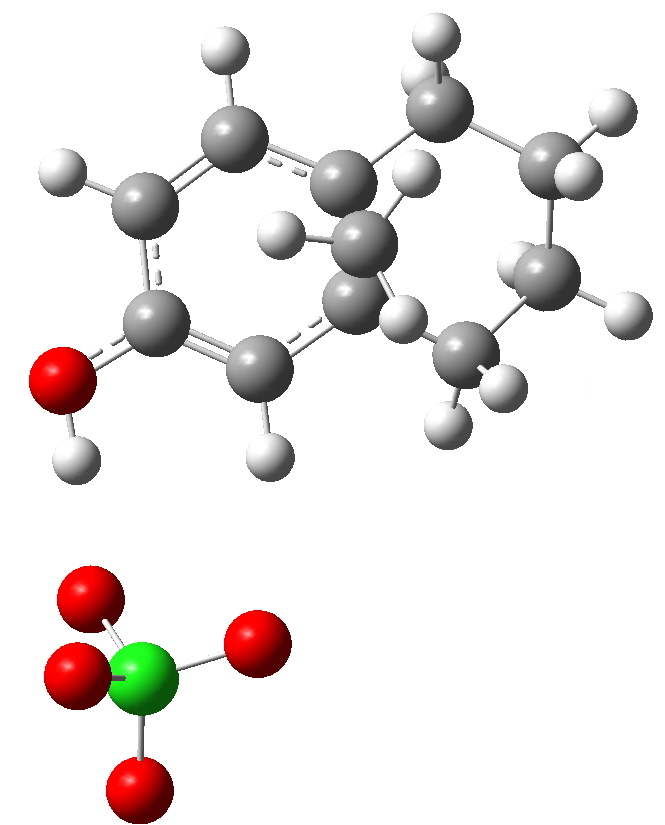
Path b-1. Click for 3D
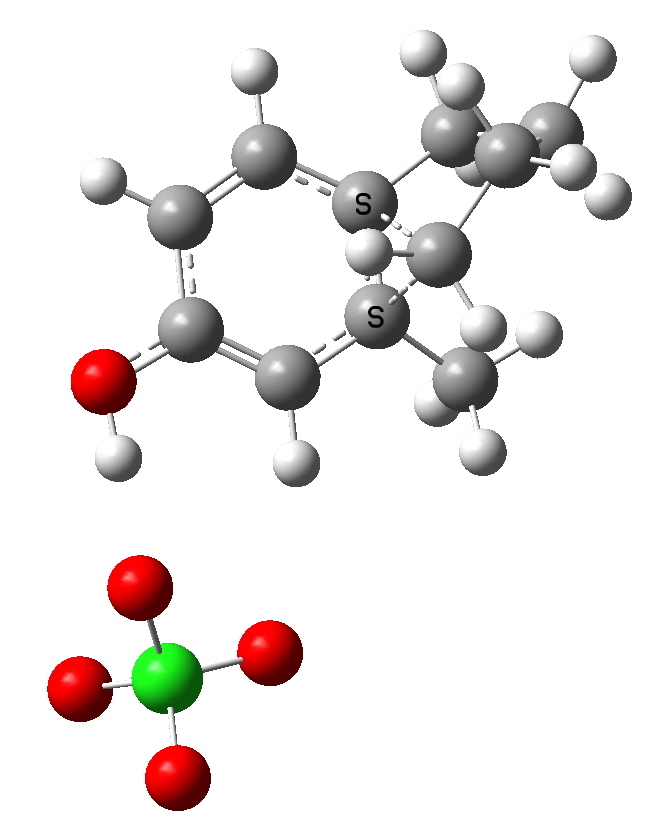
Path b-2. Click for 3D
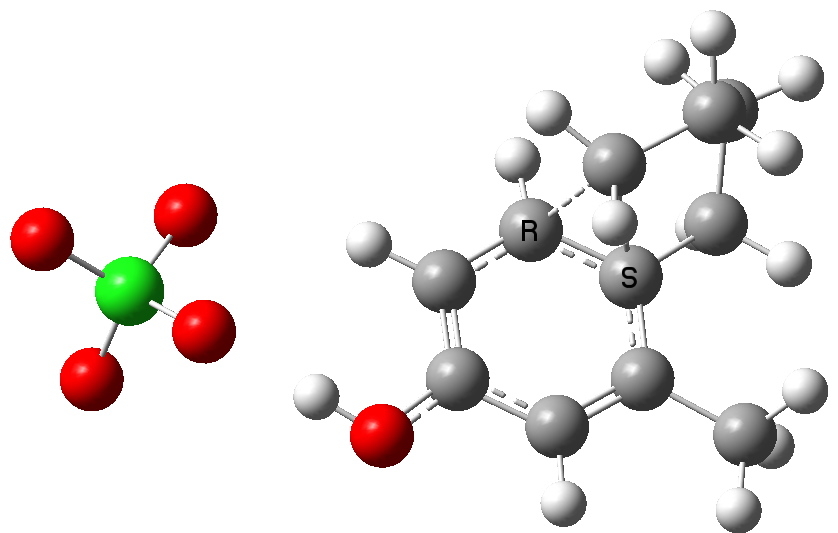
Path b-3. Click for 3D
Notice how the perchlorate counterion is relatively free to change its position relative to the substituents, and not all these positions have been explored here. This stochastic problem is an issue with counter ions (more accurately, this problem is almost always massaged away by simply ignoring this counterion. But if its ultimate positioning does matter, then one must argue that its inclusion is essential in order to build a good model).
- The energy of path (a) is thus seen to be 1.7 kcal/mol lower than (b/c), which is sufficient to favour positioning of most of the 14C tracer on * rather than * and which seems to favour the Capsi mechanism over the Futaki one, although clearly the balance between the two is a fine one. The Capsi mechanism does seem to hinge on the observation that Birch reduction of 1 reduces the blue bond entirely specifically, and the evidence for this does need to be reviewed (in an informatics sense, this evidence is buried in a string of logically connected semantic inferences, each of which may well be contained as a passing comment in a different article).
- Regarding the matter of whether path (b) or path (c) is the better representation, this goes to the heart of whether the path is respectively stepwise or concerted. The barriers for escape out of the spiro-ring intermediate defining the steps in path (b) are key. The IRC for a reaction path with a shallow intermediate is shown below.
If the depth of the well it finds itself in imparts sufficient lifetime for it to lose all (dynamic) memory of where it came from, then the probability of the * label remaining in its original position is only 50%, since the other (symmetrically equivalent but unlabeled) position may also migrate in the next step. This seems to be the case for path (b), where the intermediate is in quite a deep well (21.5 kcal/mol for escape), and this is consistent with Futaki’s experiment. If the intermediate however were to be in only in a shallow minimum (2-4 kcal/mol), the momentum it[4] inherits from the previous transition state may carry it over to the second stage without scrambling the isotope. For systems such as these, we do encounter a serious limitation of simple transition state theory, and must start to adopt a molecular dynamics approach. This might also apply to the positioning of the counterion, although perhaps less so for the relatively heavy perchlorate. It may also be an interesting issue of electron dynamics. Path (c) formally involves six electrons, path (b) only two. In a previous post, I speculated whether the electronic pack size for proton transfer was 4,6 or 8 electrons. Perhaps one day it will be possible to either measure (attosecond spectroscopy) or compute the preferred dynamics.
Postscript: I posed the question above about Capsi’s identification of the reduction product of 2. The two possible products would give different outcomes for whether the * label would be lost upon subsequent oxidation or not.
If the reaction is thermodynamically controlled, then the relative free energies of 3 and 4 would determine the outcome. A B3LYP/6-311G(d,p) calculation (in ethanol as solvent, which has a very similar dielectric to liquid ammonia) predicts 4 is about 0.3 kcal/mol lower than 3. This does not suggest that the reaction is going to be particularly regioselective, and of course Capsi’s interpretation depends on the product being entirely 4, with no 3 formed.
References
- E. Caspi, and P. Grover, "Steroids containing ring a aromatic - IV mechanism of the dienone-phenol rearrangement", Tetrahedron Letters, vol. 4, pp. 591-595, 1963. https://doi.org/10.1016/s0040-4039(01)90679-3
- E. Caspi, P.K. Grover, and Y. Shimizu, "Steroids Containing Ring A Aromatic. VIII. Mechanism of Dienone-Phenol Rearrangement", Journal of the American Chemical Society, vol. 86, pp. 2463-2467, 1964. https://doi.org/10.1021/ja01066a032
- R. Futaki, "Tracer studies on the mechanism of the dienone-phenol rearrangement with mineral acids", Tetrahedron Letters, vol. 8, pp. 2455-2458, 1967. https://doi.org/10.1016/s0040-4039(00)90831-1
- J.A. Nummela, and B.K. Carpenter, "Nonstatistical Dynamics in Deep Potential Wells: A Quasiclassical Trajectory Study of Methyl Loss from the Acetone Radical Cation", Journal of the American Chemical Society, vol. 124, pp. 8512-8513, 2002. https://doi.org/10.1021/ja026230q
- W.H. Hopff, and A.S. Dreiding, "A New Rearrangement of ar‐Tetralols with Perchloric Acid", Angewandte Chemie International Edition in English, vol. 4, pp. 690-690, 1965. https://doi.org/10.1002/anie.196506901
Tags: computational chemist, computational chemistry, Historical, pericyclic, sigmatropic shifts, tracer labelling
Hi professor!
I am an university from South Korea majoring in biochemistry and was struggling with this mysterious reaction mechanism problem. How the mothrr nature is amazing that there were so much more then Ochem2 class.
I thank you for your posting.
One small question here.
Does this rearrangement occurs if there was only a proton attached to the tertiary postion instead of the R group in picture1?