In a time when large (molecules) are considered beautiful (or the corollary that beauty must be big), it is good to reflect that small molecules may teach us something as well. Take ethane. Is there anything left which has not been said about it already? Well, consider the reaction below, in which two hydrogen atoms mutually hop from one carbon to the other.
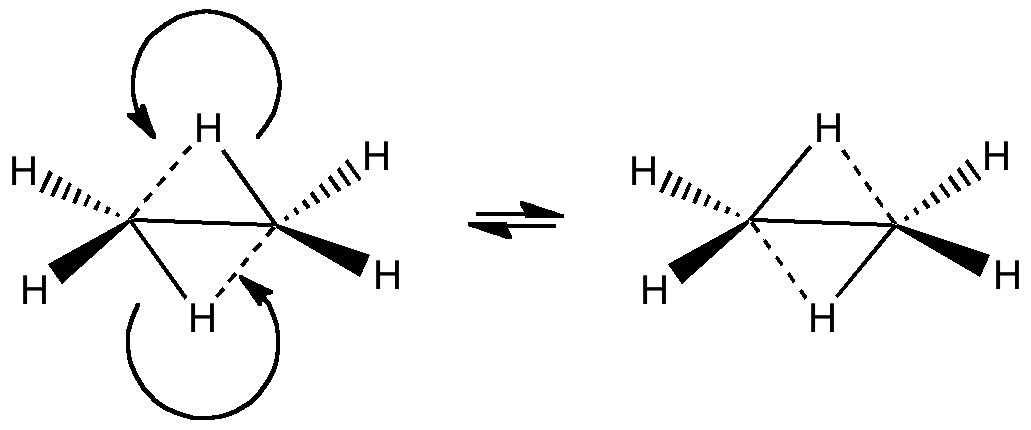
The dyotropic reaction of ethane.
This is a class of reaction known as pericyclic, in which a cyclical movement of electrons occurs in concerted fashion. Such reactions are frequently the topic of both lecture courses and book chapters. There, one is taught to count the total number of these electrons and (in some ways of teaching the subject), to apply the rules of aromaticity to the transition state describing the pericyclic reaction. I have previously described how (for themal, closed shell molecules), a 4n+2 electron count leads to aromaticity and a 4n count to antiaromaticity. In that discussion, I told of how antiaromatic molecules often go to great lengths to avoid it, and how for example cyclopropenium anion distorts to achieve this objective. Well, the above reaction, known formally as a dyotropic pericyclic rearrangement, leads to an electron count of 4, and hence belongs to our 4n rule (n=1). It must proceed through an antiaromatic transition state. Which in turn must be avoided if it possibly can.
So time for a calculation (B3LYP/6-311G(d,p) as it happens). A symmetric geometry is imposed (D2h symmetry), and this allows us to probe whether the geometry will really distort to avoid this symmetric (and hence antiaromatic) transition state.
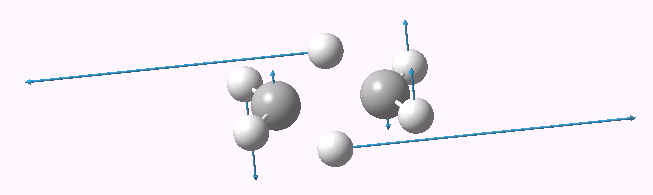
First imaginary vibrational mode for dyotropic reaction of ethane. Click for 3D.
A vibrational analysis of this geometry reveals a negative force constant corresponding to the desired motion of the two hydrogen atoms (ν 1936i cm-1, click on above for animation). But all is not what it seems; a second force constant is also negative (ν 425i cm-1). This is our distortion, in which both carbons pyramidalize, much in the manner observed previously for the cyclopropenium anion.
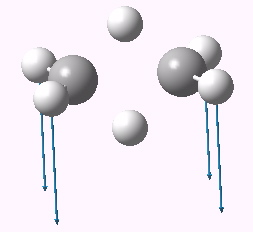
Distortive tendency for the dyotropic rearrangement. Click for 3D.
One might notice other oddities. For example, the dyotropic reaction does not (formally) involve the central C-C bond. Yet in the stationary point above, it has the distinctly odd value of 1.824Å. Here we see another type of distorsion taking place. In order to avoid the 4n electron count, some additional electrons are starting to be “borrowed” from the supposedly passive C-C bond. Indeed, following this second vibrational mode to see where it leads us gives us another stationary point looking as below, in which the central C-C bond has expanded further to 2.12Å. Those desired electrons have been well and truly borrowed, and we are now dealing with six of them, not four (and as it happens a quite different reaction).
So, ethane taught us a lot in the end. In trying to persuade it to undergo a dyotropic rearrangement, we found it came across the undesired antiaromaticity in the transition state. A nice simple example of a pericyclic selection rule in action. Of course, one could make things more complicated, but I leave that to another day.
Advanced bit: Above, I ponder whether the formal arrow pushing mechanism, which shows two arrows (= 4 electrons) might have been subverted into six electrons (=4n+2 electrons) to avoid the (formal) transition state anti-aromaticity. One (of many) methods which can tell us more or less where the electrons are and how many of them there are is ELF (electron localization function) partitioning. This is shown below for the D2h-symmetric geometry.
ELF analysis. Click for 3D.
The yellow spheres are the transposing hydrogen atoms, each carrying 1.44 electrons, in what is termed a trisynaptic ELF basin (we also know this as a three-centre-not-quite-2-electron bond). The red spheres are additional basins each carrying a further 0.74 electrons. The total number of electrons in these six (cyclically arranged) basins is 5.84. Notice in fact that in this scheme, there is no central C…C basin! Its electrons have indeed been well and truly scavenged to avoid overall anti-aromaticity (a sort of molecular democracy). Note there is no easy way of illustrating this process using arrow pushing!
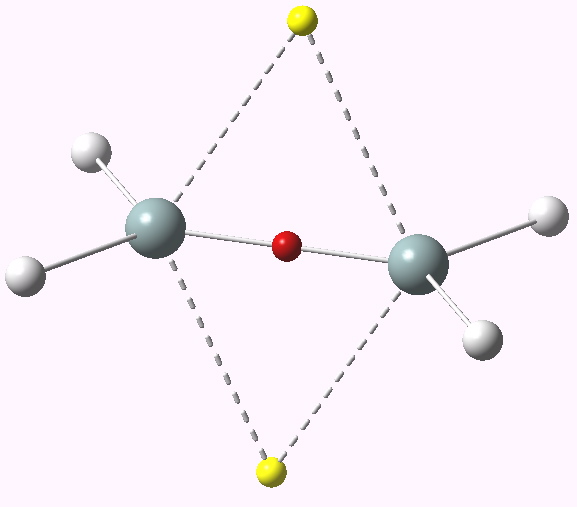
Postscript: Silicon is nowadays considered an often extreme opposite of carbon in many of its properties. Disilane is no exception. Its dyotropic rearrangement (D2h symmetry) is also a second order saddle point, having two negative force constants. The first of these is, like ethane, the dyotropic proper. But the second has a different mode for distorsion. This in fact corresponds to a disproportionation into SiH4 and SiH2.

2n -ve forc constant for dyotropic rearrangement of disilane. Click for 3D
The ELF analysis of the electrons is also different from ethane, revealing 3.67e in two three-centre Si-H-Si regions, and an Si-Si region with 2.2e. Digermane is very similar, showing carbon to be the outlier, not silicon.
One can play this game with Titanium as well (Ti2H6), a group four transition element. This shows an entirely new behaviour. The dyotropic mode force constant is no longer negative, but positive, ν 1146 cm-1. The ELF basins reveal 1.85e for the three-centre bond, and 0.47 for the Ti-Ti region (an explanation can be found in the differing nodal behaviour of the molecular orbitals, but that analysis is for another post).
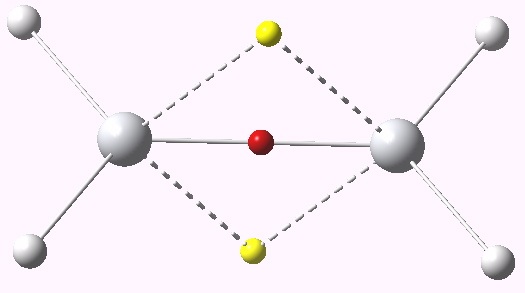
ELF analysis for Ti2H6. Click for vibration.
This postscript ends with one more system, which finally reveals a true dyotropic transition state: ethene! The two three-centre basins have 1.36e each, whilst the C-C region has 4.45e distributed interestingly enough into two basins. We have seen earlier ~6 and ~4 cyclic electron systems, this one finally is approaching ~2e.
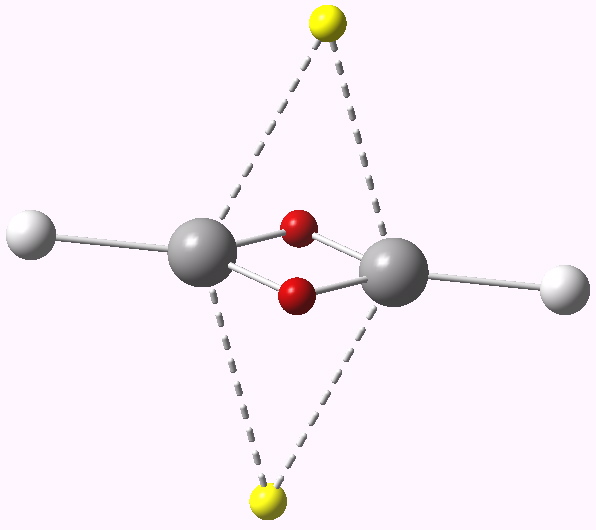
ELF analysis for ethene. Click for vibration.
Tags: animation, antiaromaticity, cyclic electron systems, distorsion, dyotropic, pericyclic, Tutorial material
[…] Henry Rzepa Chemistry with a twist « Less is more: the dyotropic rearrangement of ethane […]
[…] last two posts have played a game of find the electrons. We saw how the dyotropic rearrangement of ethane borrowed electrons from the C-C bond, and how 1,2,dibromoethane went ionic on us. How about this […]
The diagram below shows four molecular orbitals for Ti2H6 (top row) and C2H6 (bottom row).
These MOs for ethane are constructed from s/p AOs, whereas those for titane are from s/d AOs. The difference really matters for the HOMO (left). Note the nodes at the migrating central hydrogens for the former, and the absence of such nodes for the latter. This is what makes the difference between the first being a second order saddle point in the potential surface, and the latter a minimum! Note also how the difference in this HOMO explains the lack of a strong C-C bond, but the presence of a weak Ti-Ti bond. d-orbitals do make a difference!
Interesting. You find these papers I wrote with Mark Gordon relevant.
Simon P. Webb and Mark S. Gordon, “Molecular Electronic Structure and Energetics of the Isomers of Ti2H6”, Journal of the American Chemical Society, 1998, volume 120, pages 3846-3857. DOI: 10.1021/ja973195s
Simon P. Webb and Mark S.Gordon, “The Effect of Spin-Orbit Coupling on the Magnetic Properties of Ti2H6”, Journal of Chemical Physics, 1998, volume 109, pages 919-927.
Cheers,
Simon