Understanding why and how proteins fold continues to be a grand challenge in science. I have described how Wrinch in 1936 made a bold proposal for the mechanism, which however flew in the face of much of then known chemistry. Linus Pauling took most of the credit (and a Nobel prize) when in a famous paper[1] in 1951 he suggested a mechanism that involved (inter alia) the formation of what he termed α-helices. Jack Dunitz in 2001[2] wrote a must-read article[3] on the topic of “Pauling’s Left-handed α-helix” (it is now known to be right handed). I thought I would revisit this famous example with a calculation of my own and here I have used the ωB97XD/6-311G(d,p) DFT procedure[4] to calculate some of the energy components of a small helix comprising (ala)6 in both left and right handed form.
Firstly, it is important to note that Pauling was apparently not aware of the absolute handedness of amino acids (which are (S) in CIP terminology). This had in fact only been established a few months before Pauling’s publication by Bijvoet[5], and news of this might not have reached Pauling. So Pauling guessed (or perhaps, he had already built his models, and did not have time to reconstruct them) and his famous α-helix diagram[1] turned out to be the enantiomer of the real McCoy. As with DNA itself, the helix bears a diastereomeric relationship to the chirality of the amino acids; both have to be inverted to get the proper enantiomer (which is what Pauling did). The secret that Pauling had discovered was hydrogen bonding, and particular, weak N-H…O=C interactions (Wrinch had thought it was strong covalent N-C-OH bonding instead). Of course, there are other effects at work, which include van der Waals or dispersion interactions, electrostatic effects resulting from the large dipoles in peptides (not least due to the zwitterionic character), the planarity of the peptide bond itself, the potential for other types of hydrogen bond (e.g. C-H…O) and entropic effects. I have split some of these down for left and right handed forms of DNA in another post.
It turns out calculating most of these effects on an even-handed basis is not that easy. Only the recent advent of dispersion-corrected DFT procedures, together with solvation algorithms that allow for accurate geometry optimisation and subsequent evaluation of free energies allows such a calculation to be performed. Hitherto, it has been mostly molecular mechanics that has been used (which itself relies on many parameters from quantum mechanics, such as atom charges, and explicitly identifying interactions for hydrogen bonding). By returning to a quantum-mechanical model, some of these assumptions inherent in the mechanics method need not be made.
We showed in 1991[6] that an effective solvation treatment required for the zwitterionic form of amino acids in aqueous solutions would ideally comprise not only a self-consistent-reaction-field, but also explicit water molecules as solvent. Here only the former solvation term is included, but expanding the model to include water is certainly possible. Both the zwitterionic and the neutral forms of (ala)6 are included below, so that the effect of a large dipole on the structure and relative helical stability can be estimated. One notes that (even in a dielectric cavity corresponding to water), the extended zwitterions are high energy species. In a protein, they of course would be stabilized by the immediate environment of the ions. The right-handed helix clearly comes out as more stable (by about 1 kcal/mol per residue, see also[7] but this is not really due to either dispersion effects or entropy and must therefore arise largely from the hydrogen-bond like interactions. Ionizing the termini to form a zwitterion increases the propensity for a right handed helix slightly.
| Relative thermodynamic energies (kcal mol-1) of (ala)6 α-helices | |||||
|---|---|---|---|---|---|
| System | Total energy | Dispersion | ΔΔH298 | Δ(T.ΔS298) | ΔΔG298 |
| Left, neutral | 0.0 |
0.0 | 0.0 | 0.0 | 0.0 |
| Right, neutral | -4.0 |
+0.2 | -4.0 | 0.9 | -4.9 |
| Left, zwitterion | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| Right, zwitterion | -7.1 | 0.1 | -6.3 | 1.7 | -8.0 |
Shown below are the calculated structures. The chains have (inter alia) unusual bifurcated hydrogen-bonding interactions, between one carbonyl group and two N-H groups (show as atom with halo). These are not quite the models that Linus Pauling built!
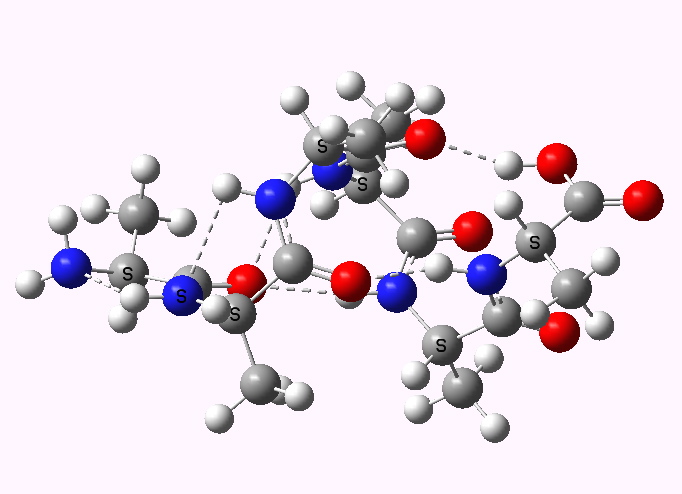 Left handed. Click for 3D |
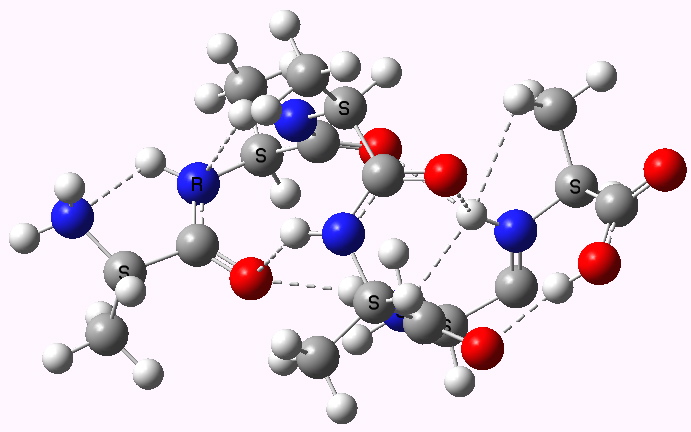 Right handed. Click for 3D |
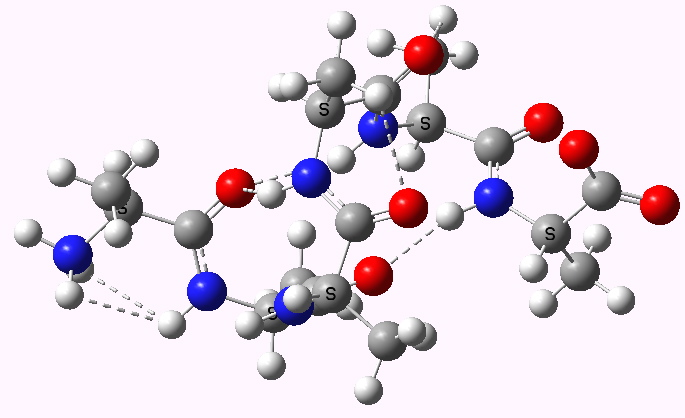 Left handed zwitterion. Click for 3D |
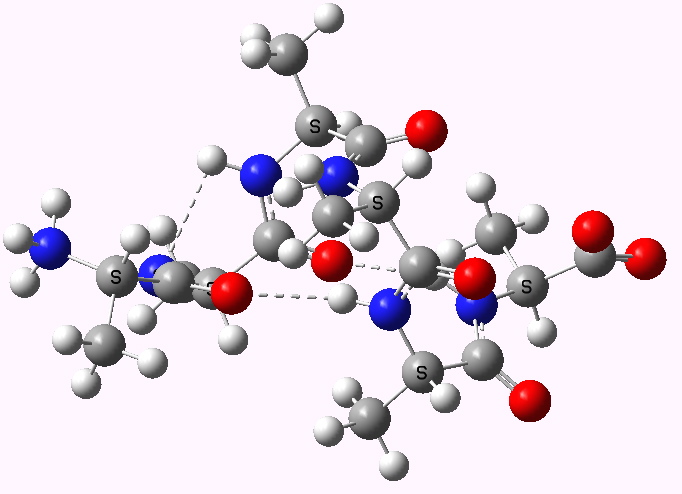 Right handed zwitterion. Click for 3D |
For a more objective analysis of the interactions within the system, a QTAIM analysis is shown below.
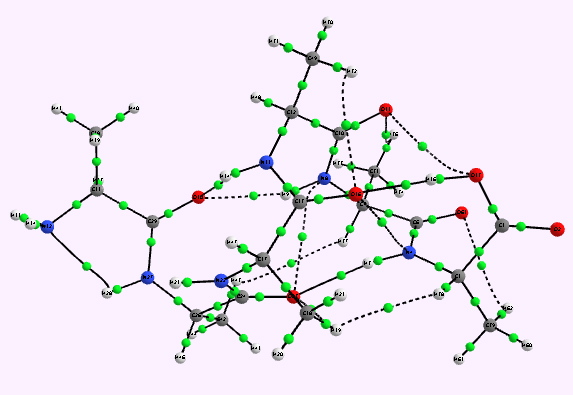 Left helix. Bond critical points in green. Click for 3D. |
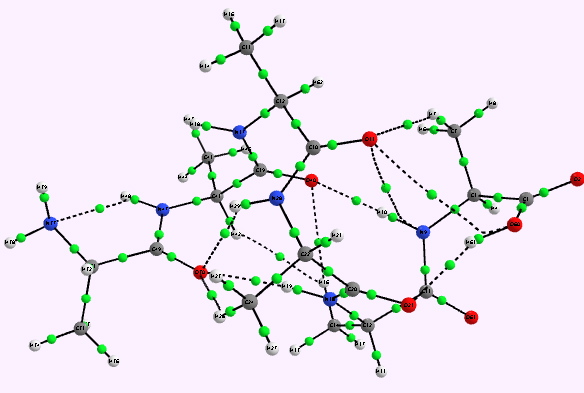 Right helix. Click for 3D |
Whilst the overall conclusion is that theory agrees well with the experimental observation that peptide sequences tend to coil into right rather than left handed helices, the reasons they do so is a little more subtle than simple model building alone can reveal. As the AIM shows, a plethora of unusual and weaker interactions occur within these helices, a full analysis of which must await presentation elsewhere.
An NCI analysis reveals strong hydrogen bonds as blue-shaded surfaces.
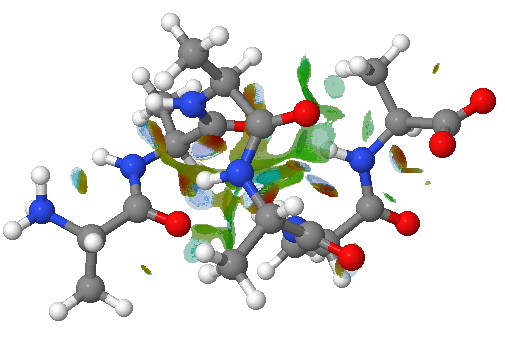
NCI surface. Click for 3D.
References
- L. Pauling, R.B. Corey, and H.R. Branson, "The structure of proteins: Two hydrogen-bonded helical configurations of the polypeptide chain", Proceedings of the National Academy of Sciences, vol. 37, pp. 205-211, 1951. https://doi.org/10.1073/pnas.37.4.205
- J.D. Dunitz, "Pauling's Left-Handed α-Helix", Angewandte Chemie International Edition, vol. 40, pp. 4167-4173, 2001. https://doi.org/10.1002/1521-3773(20011119)40:22<4167::aid-anie4167>3.0.co;2-q
- https://doi.org/
- K.S. Thanthiriwatte, E.G. Hohenstein, L.A. Burns, and C.D. Sherrill, "Assessment of the Performance of DFT and DFT-D Methods for Describing Distance Dependence of Hydrogen-Bonded Interactions", Journal of Chemical Theory and Computation, vol. 7, pp. 88-96, 2010. https://doi.org/10.1021/ct100469b
- J.M. BIJVOET, A.F. PEERDEMAN, and A.J. van BOMMEL, "Determination of the Absolute Configuration of Optically Active Compounds by Means of X-Rays", Nature, vol. 168, pp. 271-272, 1951. https://doi.org/10.1038/168271a0
- H.S. Rzepa, and M.Y. Yi, "An AM1 and PM3 molecular orbital and self-consistent reaction-field study of the aqueous solvation of glycine, alanine and proline in their neutral and zwitterionic forms", Journal of the Chemical Society, Perkin Transactions 2, pp. 531, 1991. https://doi.org/10.1039/p29910000531
- A. Banerjee, S. Datta, A. Pramanik, N. Shamala, and P. Balaram, "Heterogeneity and Stability of Helical Conformations in Peptides: Crystallographic and NMR Studies of a Model Heptapeptide", Journal of the American Chemical Society, vol. 118, pp. 9477-9483, 1996. https://doi.org/10.1021/ja960665u
Tags: alpha-helix, aqueous solutions, chiroptical, conformational analysis, dielectric, energy, energy components, high energy species, Historical, Jack Dunitz, Julia Contreras-Garcia, protein, solvation algorithms, Tutorial material, watoc11
[…] Henry Rzepa Chemistry with a twist « Why are α-helices in proteins mostly right handed? […]
[…] wrote in an earlier post how Pauling’s Nobel prize-winning suggestion in February 1951 of an […]
[…] end by reminding that the s-cis H-N-C=O conformation is a very common feature in peptides (the CCDC database comprises mostly small molecules, not larger peptides and proteins) arising from […]
Steve Connolly sent me the following information
In DOI: fdw4k6 they concluded that just 31 out of 7284 proteins displayed LH alpha helices (of >4 aa’s in length), or just 0.4% in total!
To which I add a hugely approximate estimate of the average relative energies. Taking a ratio of 7284/31 and converting to a free energy difference, one gets ~ 3.2 kcal/mol. This of course has to be normalised against the chain length.