Is there a preferred pack size for electrons on the move? Or put less flamboyantly, is there an optimum, and a maximum number of arrows (electron pairs) that one might push in revealing the mechanism of a concerted reaction? A sort of village-instinct for electrons. Consider the following (known, DOI: 10.1016/S0040-4039(00)98289-3) reaction
It is a double [3,3] sigmatropic rearrangement, each component involving two packs of three arrows (six electrons) each. Do these packs move together, or do they prefer to move one at a time? If the former, then we come up against another interesting question. How many of say the six bonding electrons in a triple bond can simultaneously participate in a reaction? Many a tutor of the arrow pushing exercise might say the limit is always two (I have even seen this written into a set of rules for arrow pushing). But could it be four, as shown in the above example? Or perchance even six as discussed in this post? OK, the question is rather loaded for this example, since being a pericyclic reaction it has a built in (thermal) preference for packs of 4n+2 electrons, which enable the transition state for the process to be considered as aromatic. So in a sense it boils down to whether two aromatic packs would have any advantage in both marauding concurrently.
A connection can also be made to recent work by Rainer Herges (DOI: 10.1021/jo801390x) in which he suggests that pericyclic reactions involving four electrons at an alkyne can indeed be concerted, giving them the specific name of coarctate reactions (ones which exhibit one or more coarctate atoms at each of which two bonds are made and two bonds are broken). And one further connection is to Clar islands, in which the tendency of electrons in polycyclic aromatic hydrocarbons (PAH) to form packs of six is discussed (these of course are not marauding).
So onwards to a computational exploration (B3LYP/6-311G(d,p), 10042/to-6354). Two geometries can be located, with respectively C2 and Ci symmetries. They differ in the orientation of the two chair-like rings, and the former (shown below) is the more (cis) stable. Two negative force constants are calculated (shown below) which indicate that the two [3,3] sigmatropic rearrangements like to go consecutively and not concurrently.
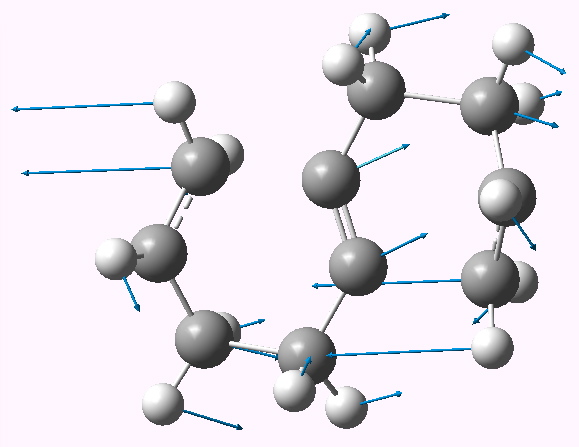 Geometry of the asynchronous pathway. Click for 3D |
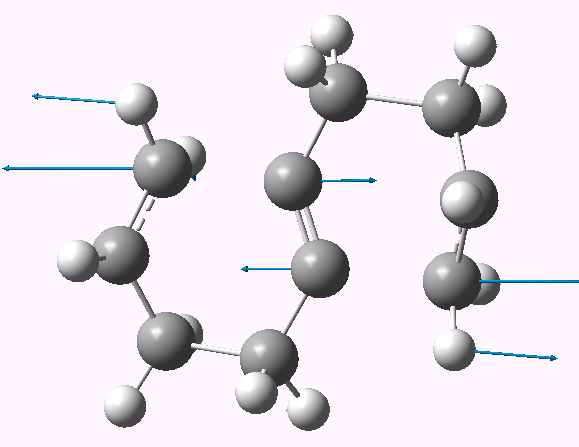 Geometry of the synchronous pathway. Click for 3D |
The ΔG† is calculated as high as 58.3 kcal/mol, which given that the reaction does proceed experimentally at ~410°C suggests this cannot be the true mechanism (discussion of which I leave to a future post). The electrons therefore move in smaller packs, but certainly not 12!
In conclusion, one might make the analogy of electrons as medieval travellers, preferring to travel in small groups, and probably invariably stopping off a in a coaching inn for a rest whenever they see one close to their route (or perhaps even sometimes well off the route). I suspect (but cannot prove) that there are few types of bond forming or bond breaking reactions which involve more than five arrows (ten electrons) participating in a single concerted step. More, and I think the travelling electrons are likely to find a resting place on the journey (which, if not a closed shell species, may well be a biradical, or in suitable solvent, zwitterion).
So that is the challenge posed here; to find an example of a reaction involving six or more arrows which theory appears to show is concerted and where new bonds are formed, or old ones broken (this last clause excludes artificial reactions such as bond shifting in higher annulenes).
Tags: Rainer Herges, tutor, Tutorial material
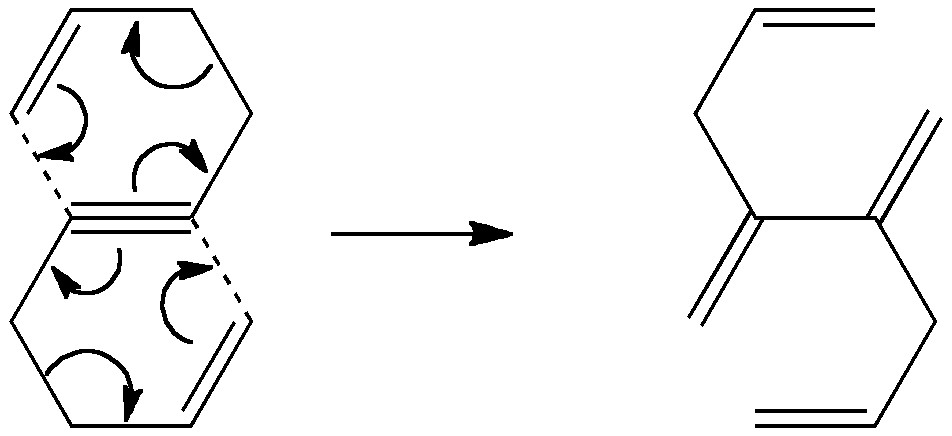
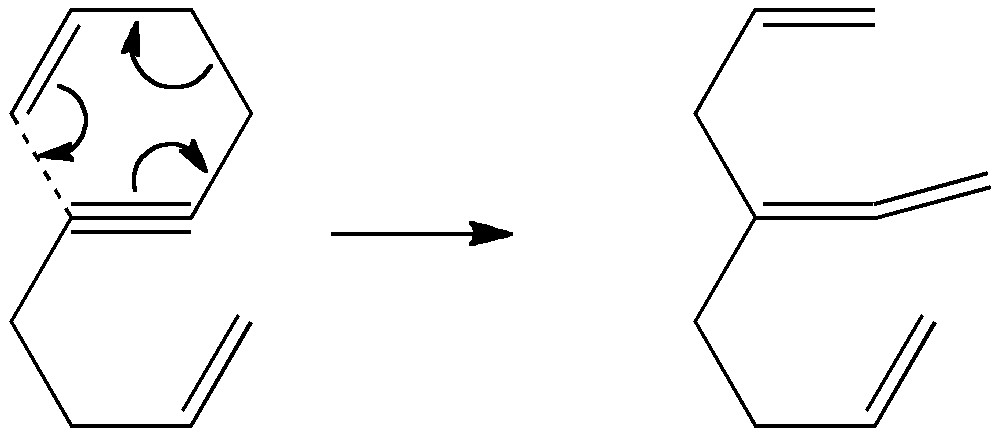
[…] steps, or one might move one at a time in four steps. These processes would involve respectively 8, 6 or 4 electrons in each step. There is a fundamental difference between the first pathway and the last two; the […]