A recently published review on hypervalency[1] introduced a very simple way of quantifying the effect. One of the molecules which was suggested to be hypervalent using this method was diazomethane. Here I take a closer look.
The new method is called the valence electron equivalent γ. It is defined as “the formal shared electron count at a given atom, obtained by any combination of valid ionic and covalent resonance forms that reproduces the observed charge distribution”. These atom charge maps can be obtained from various kinds of quantum mechanical calculation; the one adopted in the review was Bader’s QTAIM analysis.
Three resonance forms used to estimate γ for the atoms in diazomethane are shown below. According to Durrant[1], “if γ(X) > 8, neither form of the octet rule is obeyed and the atom is hypervalent”. His procedure gives γ(N) = 10 (table 3 and also structure 27a[1]), suggesting that the third resonance form shown below is the most appropriate.
As a result, the nitrogen is to be considered hypervalent, with five formal covalent bonds and hence a ten shared-electron valence shell. If such hypervalence is to be considered as more than just a convenient representation and to have a deeper underlying foundation, similar conclusions should ideally emerge from other ways of analysing the wavefunctions for such species. Here I try the NBO (Natural Bond Orbital) and ELF (Electron localization Function) analyses of two types of wavefunction using both DFT (density functional theory) ωB97XD/Def2-TZVPP and multi-reference CASSCF(12,12)/Def2-TZVPP Hamiltonians.‡
Firstly, the NBO method, which localizes electron pairs. There are four bonding NBOs associated with the central nitrogen and a modest contribution from a fifth, the terminal nitrogen lone pair (bottom).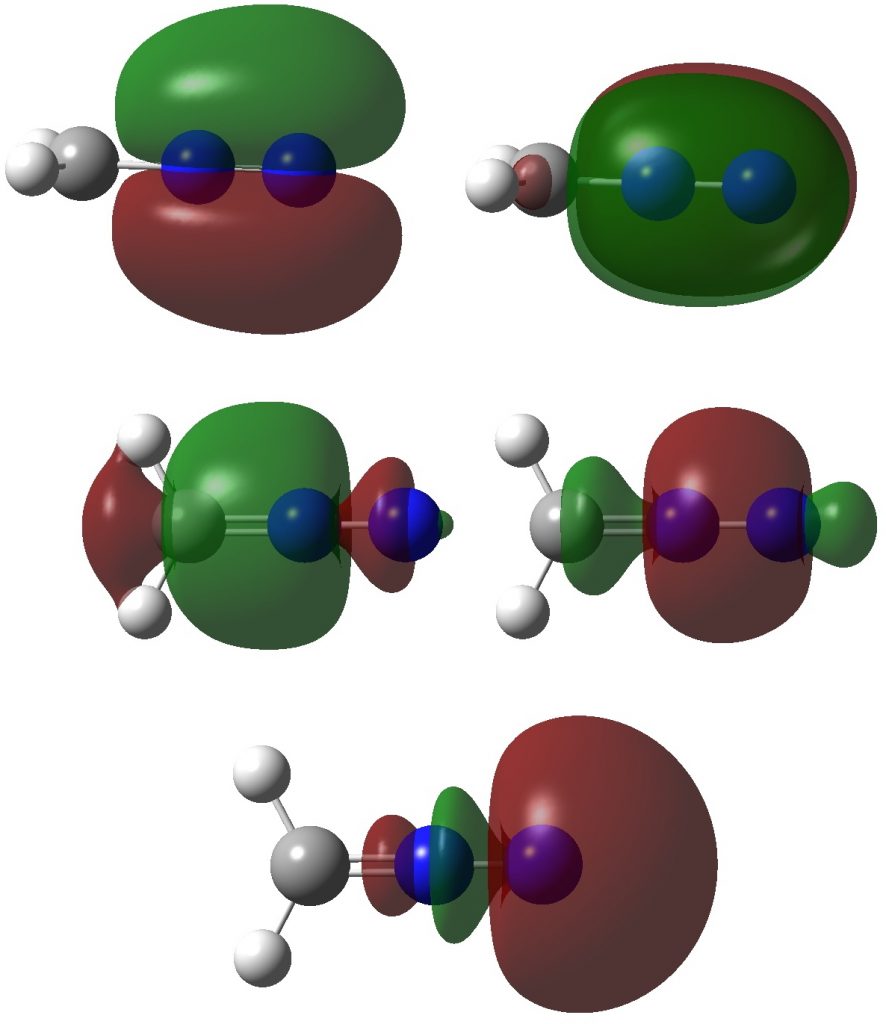
The carbon has four NBOs comprising one “non-bonding lone pair”, two C-Hs, a C-N and one partial C-N (bottom). This partitioning can be quantified using Wiberg atom bond indices: C, 3.716; N 3.802; N 2.907 (the C-N and N=N bond orders are 1.425 and 2.368). Note that the “non-bonding carbon lone pair” would not contribute to the C bond index, which is already 3.72. Is numerical evidence perhaps emerging that the carbon may exceed the octet in its valence shell? In contrast, the central nitrogen, with a bond index of 3.802, but not having any associated “non-bonding lone pair”, does not look to exceeding the octet. It seems well short of achieving γ(N) = 10, equivalent to a bond index of 5 as shown in the resonance form above.
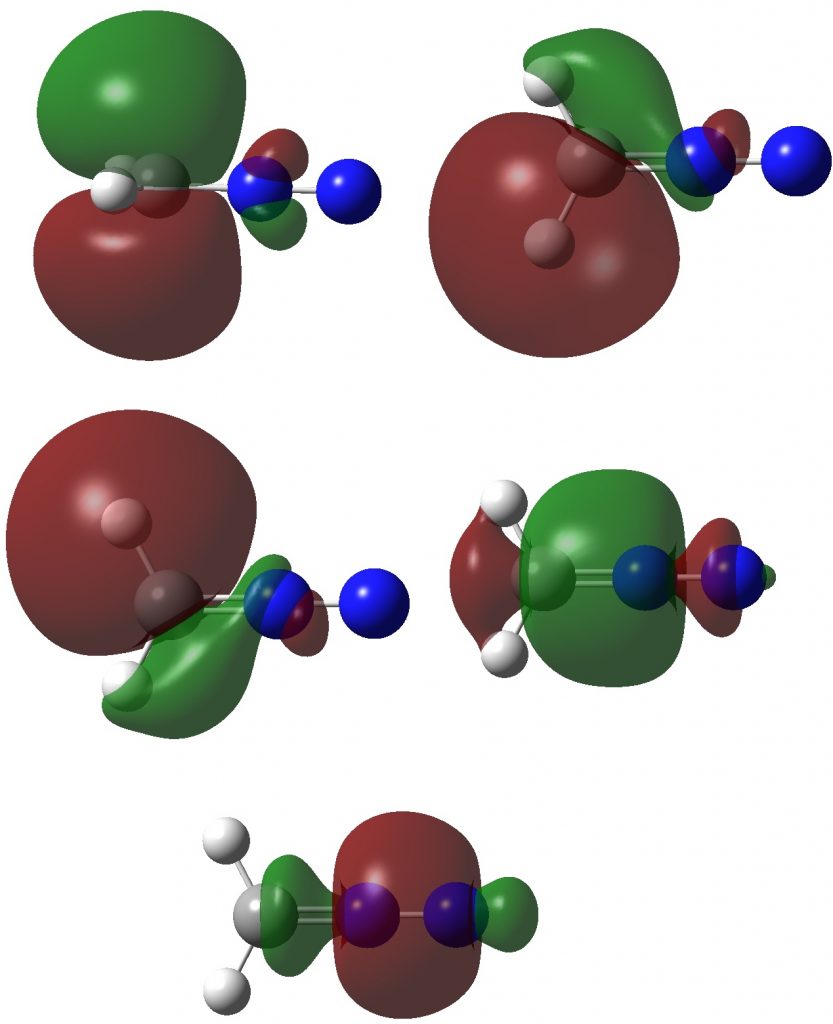
Now for ELF, which is derived from the electron density and the basin locations from its kinetic energy density. The values are the integrations for the individual ELF basins, of which 0.498*2 = 0.996 is the monosynaptic basin for the carbon lone pair noted above. The total for this carbon comes to 8.16, the adjacent nitrogen 6.59 and the terminal nitrogen 7.52e.
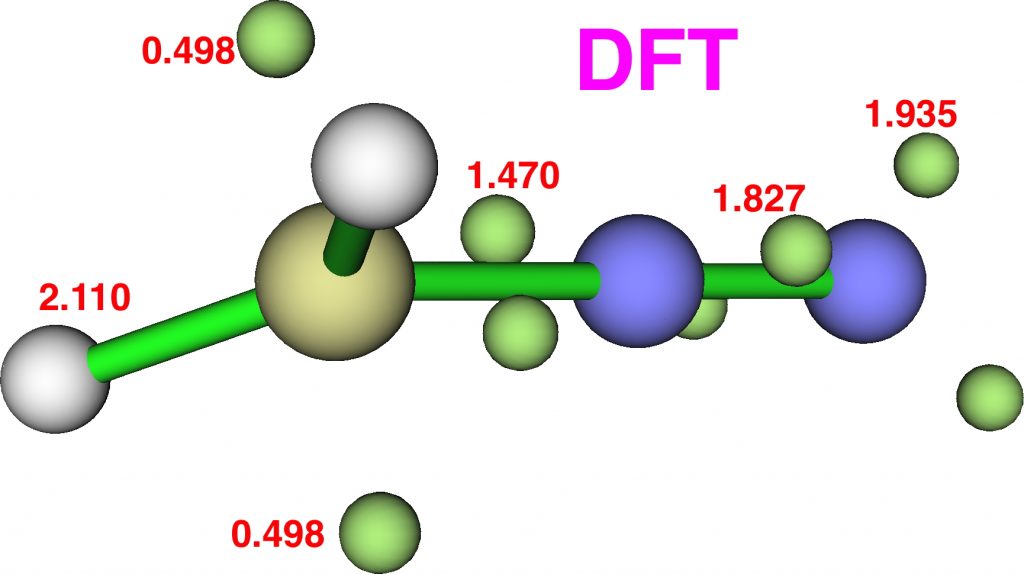
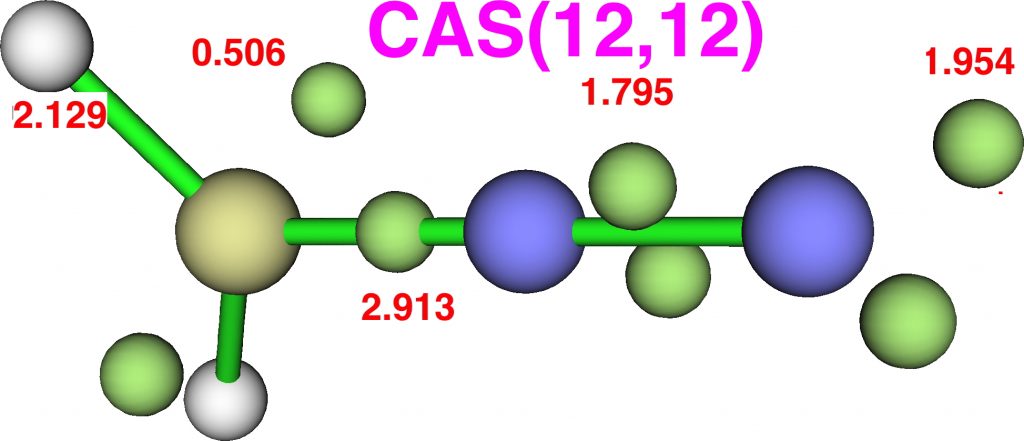
The CASSCF(12,12) values are respectively are 8.18, 6.50 and 7.50e, which are very similar. So these two types of electron partitioning show no evidence that the central nitrogen has γ(N) = 10; it’s actually ~6.5, which is a long way short of 10! However, γ(C) = ~8.2, which does exceed the octet, if only very modestly. Perhaps this can best be summarised with the following representation based on the bond orders, which indicates three shared covalent bonds to carbon, a partial (dashed) C-N interaction and a lone pair implied by the minus sign, the total of which exceeds γ(C) = ~8. It all boils down really to whether that “lone pair” of electrons on the carbon is truly a non-bonding electron pair or whether it should be considered a fully covalent pair associated also with the nitrogen. Certainly, there appears to be no evidence from NBO or ELF that this is the case.
The next logical question to ask is whether the effect can be “optimised” such that γ(C) > 8 or even >> 8. I will address this in the next post.
‡FAIR data for all calculations is available at DOI: 10.14469/hpc/3476
References
- M.C. Durrant, "A quantitative definition of hypervalency", Chemical Science, vol. 6, pp. 6614-6623, 2015. https://doi.org/10.1039/c5sc02076j
Tags: kinetic energy density