This question was posted on the CCL (computational chemistry list) by John McKelvey. Here, I give an answer in the form of a search of the CSD (crystal structure database).
I was not sure if the question related purely to the geometries obtained using computational methods or to comparisons with experimentally determined structures. Or indeed whether it related to azobenzene specifically or to azobenzenes in general. Here, I comment only in respect of the latter two. The search was defined as below, with the following specifications:
- The absolute value of the central torsion (TOR1) was constrained to 0-60° for cis azobenzenes and to 120-180° for trans azobenzenes.
- Two further torsions (TOR2, TOR3) specify the torsion angle about the aryl to N bond.
- The R factor is < 0.1, and there are no errors or disorder.
- The C-N bonds were specified as acyclic.
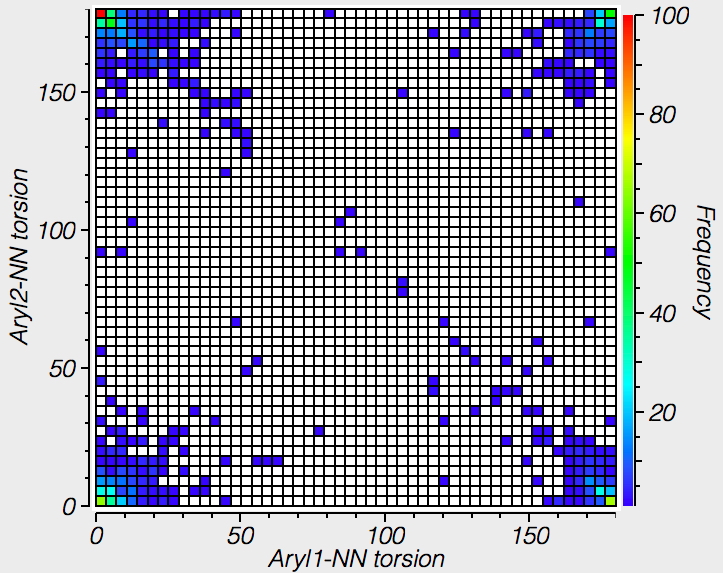
| Trans Azobenzenes, 1111 examples |
|---|
|
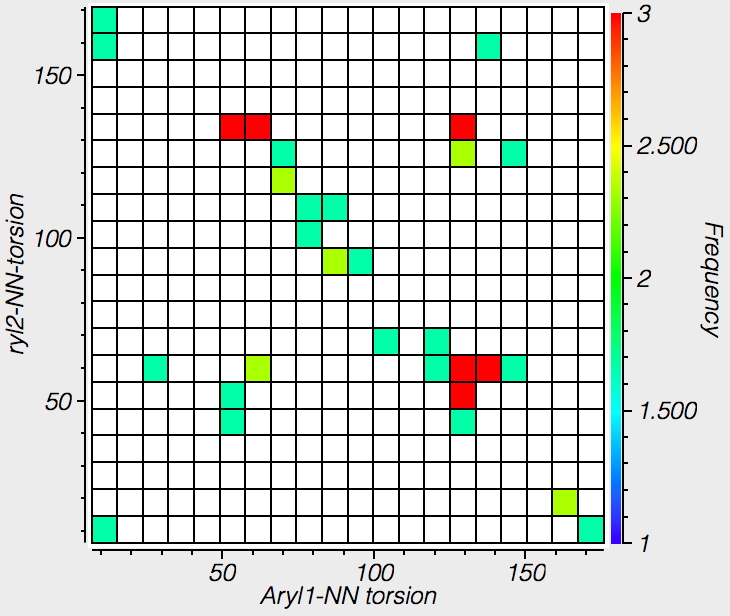
| Cis Azobenzenes, 42 examples |
|
The results show that by and large, trans azo-benzenes are co-planar to ± 30°, but there are some interesting points in the centre with dihedral angles of ~90°. Cis azobenzenes on the other hand are mostly NOT planar, with red hotspots at about 50 or 130° of twist.
These results took about 20 minutes to define, search, and plot as per above. I hope it provides John with an answer, even if it's not the one he might have meant!
Acknowledgments
This post has been cross-posted in PDF format at Authorea.
Tags: Azobenzene, John McKelvey, search azobenzene
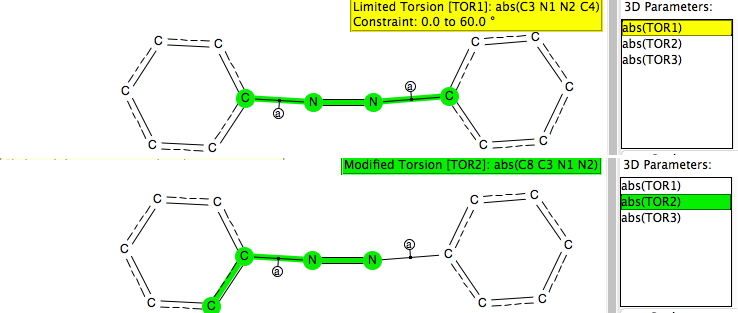
Here are the corresponding plots for imines, ie Ar-C=N-Ar' showing the torsions for both cis and trans stereochemistries, about the Ar-C and Ar-N bonds. It seems the torsion about the aryl C-N bond is a lot softer and easier than the aryl C-C bond.
A further search, this time for aryl-P=P-aryl systems. There are only a few examples of trans (and none of cis), and here the C-P dihedrals are now largely ~90°
I find this is very interesting. May I suggest another way to answer the question – with the help of Avnir's continuous symmetry measure S(Cs) for the permutation that permutes each atom with itself. It measures the distance of each structure to a structure with the same vertices and connectivity, but with Cs symmetry. The measure is zero if the structure is symmetric (i.e. planar) and rises as the structure deviates from planarity. In the attached figure I drew a torsion map similar to the one in above representing 961 fragments of azobenzene from the CSD database and colored them by their S(Cs) level. Note that the color scale is not linear. Statistically most of the structures are very closed to planarity (median S(Cs) is 0.065 and the average is 0.82). The method can also be used to distinguish between cis and trans azobenzene since they belong to different symmetry point groups.
Please see http://telem.openu.ac.il/csm/ for more details on the method.
Sincerely,
Dr. Inbal Tuvi-Arad
Department of Natural Sciences
The Open University of Israel
Thanks Inbal!!
My plots of course map to e.g. just one quadrant of the symmetry map above, since I took the absolute value of the torsion angle, whereas the diagram above includes both positive and negative values.
Well, looking carefully one can note that the symmetry map is not C4 symmetric (and only approximately C2 symmetric), therefore one quadrant is an approximation to the others. See for example the area around (-120,-120) that looks very different from the area around (-120,120) or (120,120).
sincerely,
Inbal