The layout of floor 2 of the chemistry department here contains a number of small rooms which function as tutorial areas. Each has a (non-interactive) whiteboard used by students and tutors for, inter-alia, thought-showering. It was in one such room that I found myself with three colleagues this monday afternoon. We soon all sensed something not quite right about the room; it slowly dawned that the whiteboard was entirely devoid of thoughts (it is normally left adorned with chemical hieroglyphics). Before we departed, one of our number crept up to the board and showered the following (the red bit only followed by a ?; thanks Willie!). The chemistry equivalent you might say of Guerrilla gardening. The product shown in blue below is for your benefit here. It is an example of a double fragmentation reaction; by an odd coincidence following on nicely from the previous post.
I have now found out that it represents the Eschenmoser double-fragmentation reaction to produce a medium-size macrolide ring.[cite]10.1002/ange.19790910827[/cite] It is interesting for several reasons:
- The reaction only proceeds if X=O (but not if X=CH2).‡
- from which the possible role that the anomeric effects in this region play become of interest.
- leading to the issue of whether the two fragmentations are connected in a concerted manner or are separate processes (first the green arrows, then the magenta arrows).
So, to provide a possible answer to the guerrilla tutorial on our next visit in a weeks time, I put a preview up here.
| System | ΔG298 | DataDOI |
|---|---|---|
| X=O, Reactant | 0.0 | [cite]10.6084/m9.figshare.1621347[/cite] |
| X=O, TS1 | 23.5 | [cite]10.14469/ch/191687[/cite] |
| X=O, TS2 | 14.5 | [cite]10.14469/ch/191683[/cite] |
Analysis
Reactant geometry
The reactant shows an asymmetric anomeric effect, with the X=O bond shorter (1.399Å) than the alternate C-O (1.426Å, diagram below, ωb97xd/6-311g(d,p) calculation). The C-X (X=O) bond shown cleaving in the diagram above is longer than either of the others (1.442Å) and the C-C cleaving bond (green arrow) is also longer than usual (1.563Å)
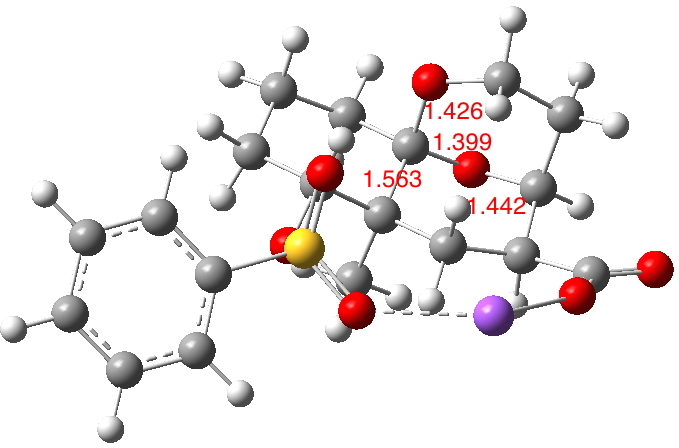
The four centres involved in the first fragmentation subtend a dihedral angle of 179.8° and the second set 177.6°. Both are therefore perfectly aligned for fragmentation. But the angle between the two fragmentations is 67.2°, meaning that they are NOT aligned correctly to occur synchronously.
Reactant NBO localised orbital analysis
The NBO interaction energy due to overlap (the black arrow above) between the oxygen lone pair (Lp) on X=O and the adjacent C-O* orbital is 16.4 kcal/mol, whereas the reverse interaction from the other oxygen is 10.1 kcal/mol due to a slightly worse anti-periplanar alignment. The NBO E(2) interaction term between the lone pair (Lp) on X=O and the adjacent about-to-fragment C-C* orbital is also relatively large at 6.6 kcal/mol, whereas that for the non-fragmenting C-C* orbital is 4.4 kcal/mol.
Reactant ELF-based lone pair analysis
In order to estimate the dihedral (antiperiplanar) angle between two atoms (more accurately the anti bond between them) and an electron lone pair on the adjacent oxygen, one needs the coordinates of the oxygen lone pair (Lp). These can be obtained using a localising technique called ELF (electron localisation function). The values are as follows:
- X=O, Lp with anomeric C-O bond: 177°
- X=O, Lp with fragmenting C-C bond: 174°
So the reactant is already pre-disposed to the green+black fragmentation due to both of the X=O:: lone pairs, hence accounting for why only this substituent shows this reaction. It also hints the first fragmentation (green arrows) is pre-disposed to start before the second one (magenta arrows).
Energies and conclusion
ΔG‡ can be obtained for two discrete transition states (green, TS1 and magenta TS2 steps), the first being distinctly the higher in free energy and corresponding to a reasonable rate reaction at elevated temperatures.
The problem illustrates nicely the importance of aligning reaction centres correctly, and how a lone pair can influence the result.
‡The corresponding free energy activation barrier for X=CH2 is 25.6 kcal/mol[cite]10.14469/ch/191701[/cite],[cite]10.14469/ch/191697[/cite]. Transposing C=CH2 with the remaining oxygen (an untried experiment) gives a barrier of 25.4 kcal/mol.[cite]10.14469/ch/191708[/cite]