I love experiments where the insight-to-time-taken ratio is high. This one pertains to exploring the coordination chemistry of the transition metal region of the periodic table; specifically the tetra-coordination of the series headed by Mn-Ni. Is the geometry tetrahedral, square planar, or other? One can get a statistical answer in about ten minutes.
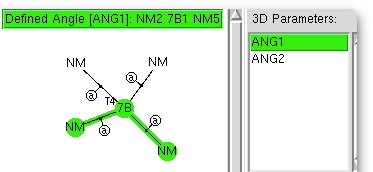The (CCDC database) search definition required is shown above. The central atom defines the column of the period table, it is specified to have precisely four other atoms bonded to it, which can be any other element. These four bonds are specified as acyclic (to avoid any bias introduced by rings). And two angles are defined subtending the central atom. And off we go, defining on the way that the hits must be refined to an R-factor of < 0.05, have no disorder, and no errors.
Mn, (Tc), Re
Fe, Ru, Os
Co, Rh, Ir
Ni, Pd, Pt
Square planar coordination will manifest with pairs of angles of either 90° or 180°, whilst tetrahedral coordination will reveal only 109°.
- Both the Mn and the Fe series show a (red) hotspot at the tetrahedral value.
- The Co series shows a tetrahedral hot spot AND a somewhat less abundant square planar double-hot spot for the combination 90/180 and 180/90.
- The Ni series reveals the hottest spots to correspond to square planar, but with a significant tetrahedral cluster.
This quick survey can be followed up by more detailed explorations of the clusters. For example, can one go to the literature and find out the typical spin state for e.g. the Ni series in each of the geometries. Unfortunately, the CCDC database does not record what the spin state of any individual compound is; one will have to go to the original literature to find out. What a shame that the linkage between two quite different properties is (as far as I know) not available in any easily searchable form. Alternatively, one can narrow down the searches to individual searches of row 1, 2 or 3 of the transition series and then compare the behaviour. The possibilities are considerable.
Then there are the outliers in each plot. Some (many?) may prove to be due to faulty data (whilst we have specified no errors, they can still occur) but others may be due to an unusual structural feature, or perhaps even an as yet unrecognized phenomenon! Set as a student experiment, one might ask each student to explore say 3 outliers and express an opinion as to what causes them to deviate. Enjoy!
Acknowledgments
This post has been cross-posted in PDF format at Authorea.
Tags: data, Pt[/caption] Square, search definition, transition metal region