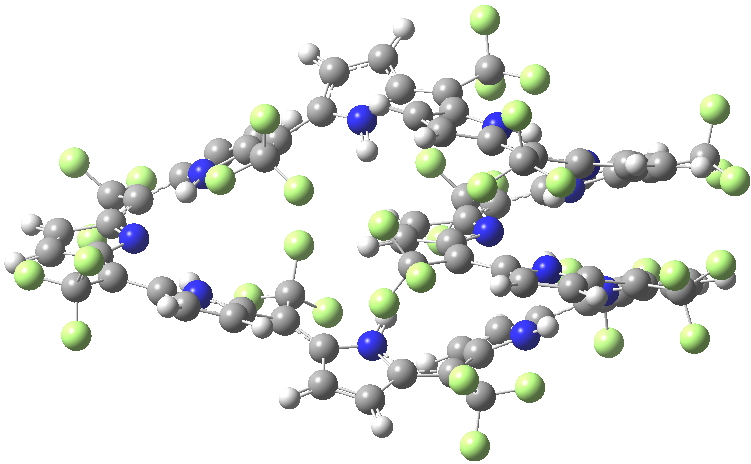
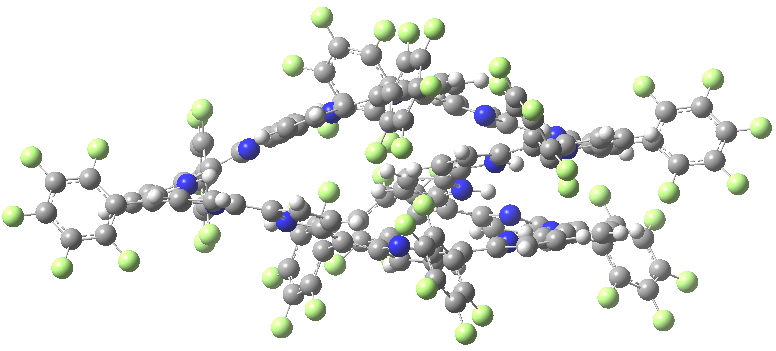
An extensive discussion developed regarding my post on a fascinating helical [144]-annulene. Topics included the nature of the ring current sustained by the π-electrons and in particular the bond-length alternation around the periphery and whether this should alter if the electron count were to be changed to that of a 4n+2 system (i.e. a dication). Whilst the [144]-annulene itself is hypothetical, it emerged that some compounds known as expanded porphyrins have very similar (albeit smaller scale) helical structures. X-ray structures for two such provide useful reality checks on the calculations. Here‡ I include the (3D) coordinates of these two systems so that you can explore for yourself their helicity.
SELQUW. Click for 3D X-ray structure
HIYTAL. Click for 3D X-ray structure
I include below Δrmeso, being the mean unsigned difference in bond length (Å) at the meso positions of the porphrin ring, the calculations being at the 6-311G(d,p) level using the DFT procedure indicated below. The linking number analysis[cite]10.1021/ja710438j[/cite] for such systems will be reported elsewhere.[cite]10.1021/ol703129z[/cite]
| Method | SELQUW | HIYTAL |
| X-ray | 0.048 | 0.045 |
| B97D/6-311G(d,p) | 0.025 | 0.015 |
| B3LYP/6-311G(d,p) | 0.047 | 0.017 |
‡The WordPress system operated here does not enable 3D coordinates to be inserted into the comment section of a post, only the main body.
Tags: Helical annulenes, X-ray
I tried to start optimizing SELQUW. It is quite laborious to extract the coordinates from the jmol applet. I had to go the show-> cif file, then copy paste with left mouse middle mouse into emacs. Babel did not work with that cif file, so I needed platon and then manually edit the lis file to make it an xyz file. I looked ok but when I started to calculate it turned out, that there is an uneven number of electrons in the neutral system?
I think it might be easier to use the digital repository links associated with the table above. I have also replaced the Jmol invocation with one using the signed applet. This should produce further menus, including one which invokes a file save dialog. I really should do this for all the posts!
Yes, I tried that one. But then only some kind of text-viewer opens up. But then from that one I was not able to save anything, instead I had to do the copy&paste. Maybe its my old ice-weasle making problems with java!?
The Δrmeso value for SELQUW at MARIJ-RI-BP86/SV(P) is 0.024.
Here is the 13th a2 MO of [((CH)9)17)]3+ in D17:

How is that possible?
In response to “The Δrmeso value for SELQUW at MARIJ-RI-BP86/SV(P) is 0.024.”, that is in good agreement with the value using B97D reported above (0.025) using a slightly different basis set, with of course the experimental value being 0.048Å.
In response to “Here is the 13th a2 MO of [((CH)9)17)]3+ in D17:” one needs to look at the linking number of the system. This chiral descriptor describes the helicity of the system. Each complete helical turn corresponds to a linking number of ±2π. If one expresses the linking number in units of ±1π, then a system with an even linking number gives rises to torus links in the π-electron density, and normally also a single molecular orbital can also be found with this topology. Such an orbital is the one shown above. So this system has an integer number of helical turns and has (in units of 1π) an even linking number. As such therefore it will be “aromatic” if 4n+2 π-electrons circulate and “antiaromatic” if 4n π-electrons circulate.
To generate a system with an odd (in units of 1π) linking number, it has become clear that we need to build a system with an half-integer number of helical turns (in units of 2π). Such a system would sustain a torus knot in the π-electron density, and this cannot be represented with just a single MO; one needs to add two MOs to do this.
Building such a model is the challenge for your coordinate building skills Raphael!
I have worked out the linking numbers for the two molecules we are considering here, namely SELQUW and HIYTAL. To show the associated 3D coordinate model, I need to put up another post, since I have not figured out how to make such models display in the window of a comment, such as this one.
Yes, I got the same idea about a treefoil knot. Then we are in D3 and get probably the same frontal orbital situation like in D17, namely the half filled e1 shell. Problem will be that the symmetry is much lower then and we probably need more atoms to get a nice unstrained system.
Another thing: Dealing all the time with Hamitonians we forget about the other big discovery of the congenial Irish mathmatician, the quaternions!
There is something called “Quaternionenmaschine” in German. It shows nicely how to do the book keeping right about turns and twists.
We need odd powers of “k”. And k = ji =ji.
I missed “the half filled e1 shell for the 4n electron case”.
I just started a [B60]2+ treefoil knot. Starting coords are here:
http://www.chem.helsinki.fi/~berger
I just bulit a paper model of a treefoil knot with my kids and we figured out that it is not a pi/-pi linkage but a 0pi one. I am afraid there is no elegant way of circumventing the “localization” of the Möbius twist.
A molecular trefoil knot, as shown in this post has a linking number of 6π and this is decomposed into Tw = -0.8π and Wr = +6.8π. So this indeed is NOT a system with an odd linking number. This molecule is unusual because the twist (Tw) and the writhe (Wr) are actually of opposite signs!
Perhaps systems with half-helical turns (as required) can only be constructed if the restriction of all cis-alkenes is supplemented with some trans-motifs?
Some examples of (4n π-electron) molecules with odd linking numbers can be found in this article, but these contain trans as well as cis alkene bonds. This table also includes the NICS(0) value, which indicates that they are all diamagnetic (and hence what we refer to as aromatic). By the way, the systems of D5 and D7 symmetry were not stable minima; the latter for example was a transition state for bond shifting. But this might just be because it is so small, and a larger ring may behave differently.
Re “Dealing all the time with Hamitonians we forget about the other big discovery of the congenial Irish mathmatician, the quaternions!” A lovely connection Raphael. I know that Bob Hanson has played with quaternion coordinates for large molecules, but I did not make the connection with using them for helical systems until you pointed it out above!
We, as chemists, do not use quaternions enough!