Although the small diatomic molecule known as dicarbon or C2 has been known for a long time, its properties and reactivity have really only been determined via its very high temperature generation. My interest started in 2010, when I speculatively proposed here that the related isoelectronic species C⩸N+ might sustain a quadruple bond. Shortly thereafter, a torrent of theoretical articles started to appear in which the idea of a quadruple bond to carbon was either supported or rejected. Clearly more experimental evidence was needed. The recent appearance of a Chemrxiv pre-print entitled “Room-temperature chemical synthesis of C2“.[1] claims to provide just this! Using the synthetic scheme outlined below, they trapped “C2” with a variety of reagents (see Figure 2A in their article), concluding that the observed reactivity best matched that of singlet “biradicaloid” C2 sustaining a quadruple bond.
Inspired by the report of this chemical synthesis, I thought I would revisit C⩸N+ to speculate how it too might be made. A colleague (thanks Ed!) had alerted me to a probably ultimate method for generating cations using tritium.[2] Radioactive decay♥ loses an electron by β emission and forms He+, which is followed by expulsion of a helium atom to leave behind a cationic centre; in this example at the sp-carbon of an alkyne.
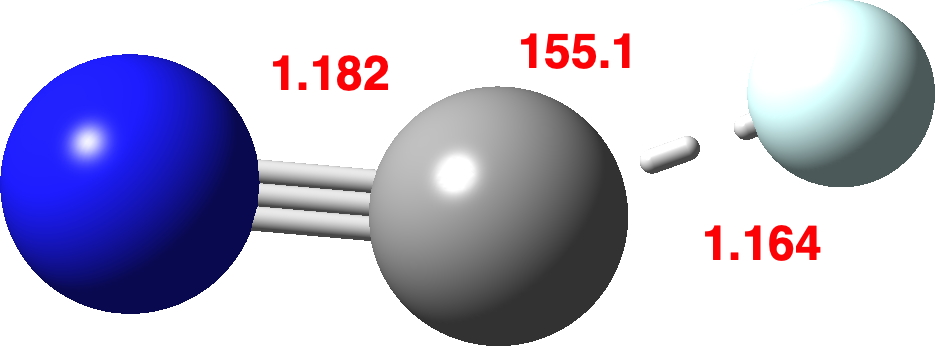
So on to explore the energetics of generating cationic C⩸N+ by this synthetic/nuclear-decay method†. The thermochemistry of the reaction (N≡C-T →) N≡C-He+ + e → N≡C+ + He ⟺ C⩸N+ will be calculated using the CCSD(T)/Def2-TZVPP method.‡ Firstly the geometry of N≡C-He+, which is bent and not linear.. This species sustains a short C-He bond, which has a calculated Wiberg bond order of 0.67. Recollect the excitement when a report appeared of bonded helium, which has a computed bond order of just 0.15! The C-He stretch in N≡C-He+ is 907 cm-1 with the bend being 193 cm-1 and the C≡N stretch 2116 cm-1.
Click image to view 3D animated model
A He atom is then lost, resulting in an exo-energic ΔΔG298 of -12.6 kcal/mol (see FAIR data DOI: 10.14469/hpc/5691). Despite all that energy injected by a nuclear decay process, together with the supercharged leaving group, the reaction is only moderately exo-energic.
Is this experiment a viable method for generating C⩸N+ cations? Since the half-life of T, aka 3H, is ~11 years, any experiment must be run for months to generate detectable amounts of products (six months as reported here[2]). The C⩸N+ must therefore be trapped as soon as it is formed. The selection of the chemical traps (avoiding HCN itself?) which could demonstrate the nature of this species will therefore be an interesting challenge, should anyone wish to try this experiment.
♥A similar procedure was used to generate the hitherto elusive perbromic acid by β decay of 83Se into 83Br. †The thermochemistry for the method reported here[1] will be explored separately. ‡The second of the two consecutive experimental C-H BDEs (bond dissociation energies) for the reaction H-C≡C-H → H-C≡C• and then H-C≡C• → C⩸C is known experimentally to be about 20 kcal/mol lower than the first. This observation is most simply explained by the formation of a 4th bond, here represented by ⩸. If you are interested in how to invoke this and other chemically useful glyphs, see here. Such thermochemistry was previously evaluated using correlated methods[3] such as CCSD(T) and MRCI (multi-reference configuration interaction, used specifically for C2); procedures which reproduced well these relative experimental BDEs.[3] Here (see FAIR data DOI: 10.14469/hpc/5684) I found that using single reference CCSD(T)/Def2-TZVPP throughout also gives a similar result, the second BDE being ~22 kcal/mol less than the first. Accordingly, this method is here used to estimate the geometry and energy of N≡CHe+ and its carbon-helium bond-dissociation to give C⩸N+ + He. I recognise that ultimately, multi-reference methods should also be used to check these results.
References
- K. Miyamoto, S. Narita, Y. Masumoto, T. Hashishin, M. Kimura, M. Ochiai, and M. Uchiyama, "Room-Temperature Chemical Synthesis of C2", 2019. http://dx.doi.org/10.26434/chemrxiv.8009633.v1
- G. Angelini, M. Hanack, J. Vermehren, and M. Speranza, "Generation and trapping of an alkynyl cation", Journal of the American Chemical Society, vol. 110, pp. 1298-1299, 1988. http://dx.doi.org/10.1021/ja00212a052
- D. Danovich, P.C. Hiberty, W. Wu, H.S. Rzepa, and S. Shaik, "The Nature of the Fourth Bond in the Ground State of C2: The Quadruple Bond Conundrum", Chemistry – A European Journal, vol. 20, pp. 6220-6232, 2014. http://dx.doi.org/10.1002/chem.201400356
Tags: Interesting chemistry
You could prepare C⩸C with C-14 at one end. The experiment might take a rather long time to produce a result though!
With modern flow techniques you MIGHT be able to use C-15 though?
Mike,
Talks us through what labelling one end of C⩸C would demonstrate.
Beta decay of C-15 would yield CN+ ions, in a similar way to TCN but without the complication of expelling He, and much faster decay. I suspect this decay (t1/2 ~ 2.5 sec) would be too fast for practical experiments though.
I’ve read about diazotizations done as flow reactions. Suppose you diazotize cyanamide? Does N≡C-N≡N+ decompose to N⩸C+?
[Sorry, couldn’t get it to type a triple bond symbol.]Energies easily calculated (might take a day or so).Update: The ωB97D/Def-TZVPP/SCRF=DCM dissociation free energy is ΔΔG +128.1 kcal/mol. The CCSD(T)/Def-TZVPP/SCRF=DCM value is +90.0 kcal/mol.
Results such as this tend to suggest that formation of these unusual “quadruple-bonded” diatomics is going to be very difficult by chemical processes alone.
A note on the state of quantum computing. I used a regular 2019 iMac (not the faster Pro model) desktop computer with 16 processors, 24Gbyte of 2666 MHz DDR4 memory and a modern SSD. The CCSD(T) calculation took 38 minutes of elapsed time to optimise the geometry and then go on to calculate the frequencies using numeric derivatives. If analytic derivatives were available, it would obviously be faster. So the sort of question you posed can be answered at a reasonably “high level” in an elapsed time of ~2 hours. Bear in mind however that a CCSD(T) calculation does scale as around the 7th power of the total number basis functions, so as the size of the molecule increases the calculation slows very quickly! In this example, the symmetry also helps!