Sometimes the originators of seminal theories in chemistry write a personal and anecdotal account of their work. Niels Bohr[cite]10.1007/BF01326955[/cite] was one such and four decades later Robert Woodward wrote “The conservation of orbital symmetry” (Chem. Soc. Special Publications (Aromaticity), 1967, 21, 217-249; it is not online and so no doi can be given). Much interesting chemistry is described there, but (like Bohr in his article), Woodward lists no citations at the end, merely giving attributions by name. Thus the following chemistry (p 236 of this article) is attributed to a Professor Fonken, and goes as follows (excluding the structure in red):
A search of the literature reveals only one published article describing this reaction[cite]10.1021/jo00238a023[/cite] by Dauben and Haubrich, published some 21 years after Woodward’s description (we might surmise that Gerhard Fonken never published his own results). In fact this more recent study was primarily concerned with 193-nm photochemical transforms (they conclude that “the Woodward-Hoffmann rules of orbital symmetry are not followed”) but you also find that the thermal outcome of heating 4 is a 3:2 mixture of compounds 5 and 6, and that only 6 goes on to give the final product 7. It does look like a classic and uncomplicated example of Woodward-Hoffmann rules.
So let us subject this system to a “reality check” (ωB97XD/6-311G(d,p) calculations). The transform of 4 → 5 rotates the two termini of the cleaving bond in a direction that produces the stereoisomer 5, with a trans alkene straddled by two cis-alkenes[cite]10.6084/m9.figshare.704833[/cite]. The two carbon atoms that define the termini of the newly formed hexatriene are ~ 4.7Å apart; too far to be able to close to form 7.
| 4 → 5 | 4 → 6 |
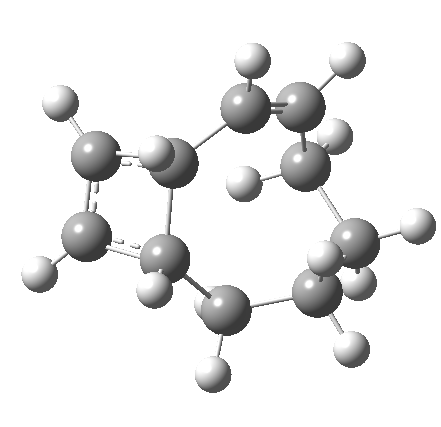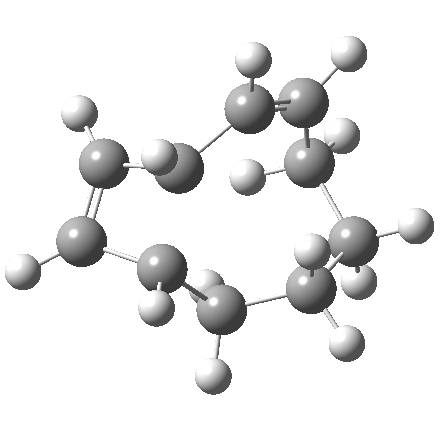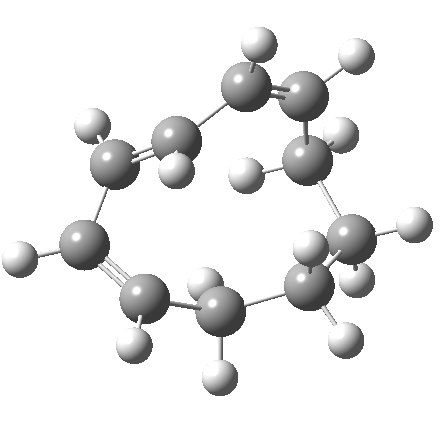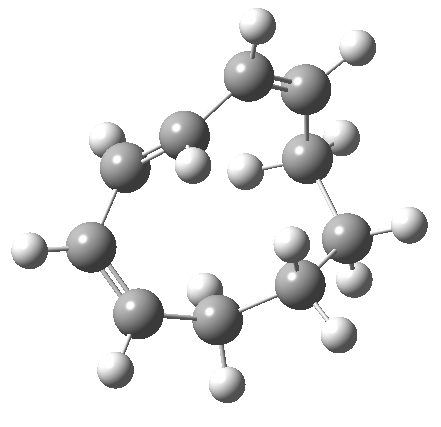 |
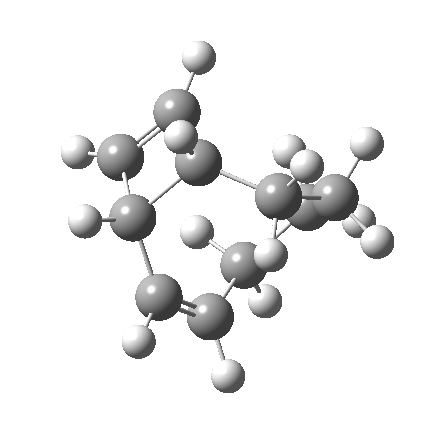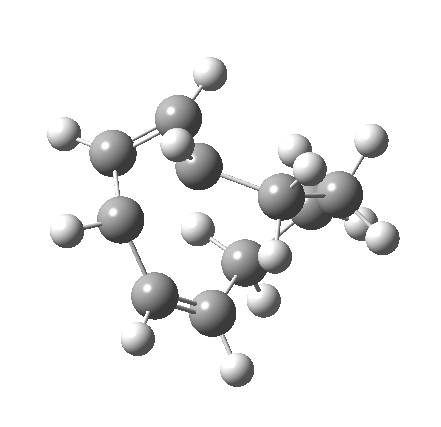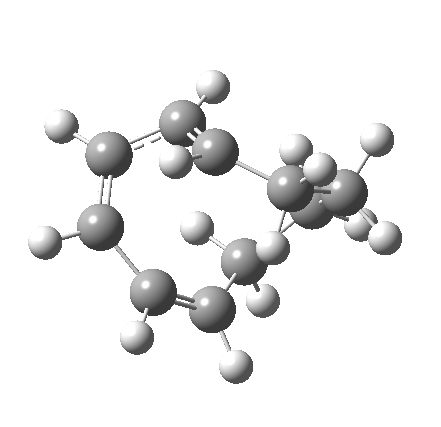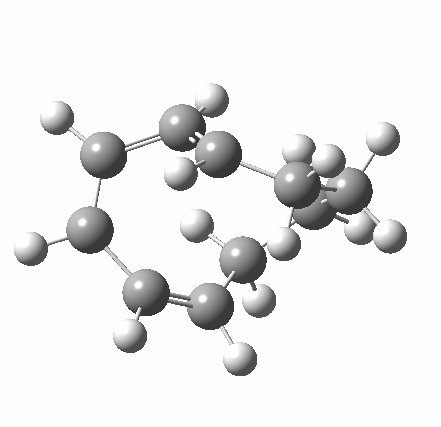 |
But with any electrocyclic reaction, two directions of rotation are always possible, and it is a rotation in the other direction that gives 4 → 6[cite]10.6084/m9.figshare.704834[/cite], ending up with a hexatriene with the trans-alkene at one end and not the middle (for which the free energy of activation is 3.1 kcal/mol higher in energy). Now the two termini of the hexatriene end up ~3.0Å apart, much more amenable to forming a bond between them to form 7.
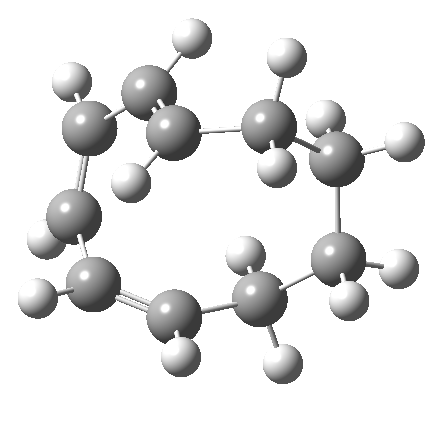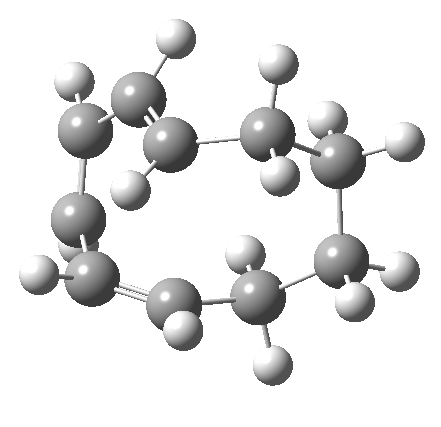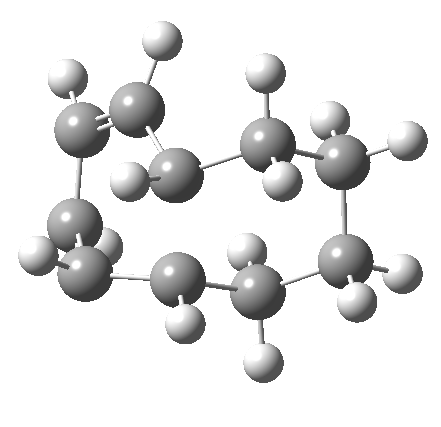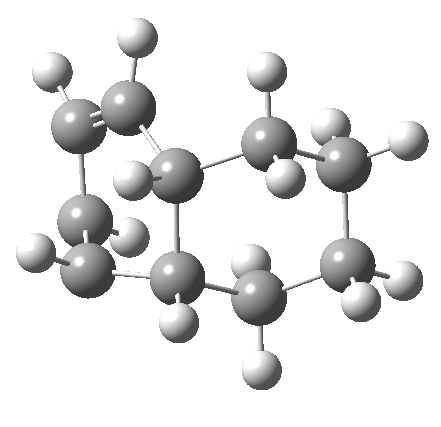
It is at this point that the apparently uncomplicated nature of this example starts to unravel. If one starts from the 3.0Å end-point of the above reaction coordinate and systematically contracts the bond between these two termini, a transition state is found leading not to 7 but to the (endothermic) isomer 8.[cite]10.6084/m9.figshare.704755[/cite]This form has a six-membered ring with a trans-alkene motif (which explains why it is so endothermic).
| 6 ↠ 8 | |
|---|---|
 |
|
Before discussing the implications of this transition state, I illustrate another isomerism that 6 can undertake; a low-barrier atropisomerism[cite]10.6084/m9.figshare.704754[/cite] to form 9, followed by another reaction with a relatively low barrier, 9 ↠ 7[cite]10.6084/m9.figshare.704844[/cite]to give the product that Woodward gives in his essay.
| 6 ↠ 9 | |
|---|---|
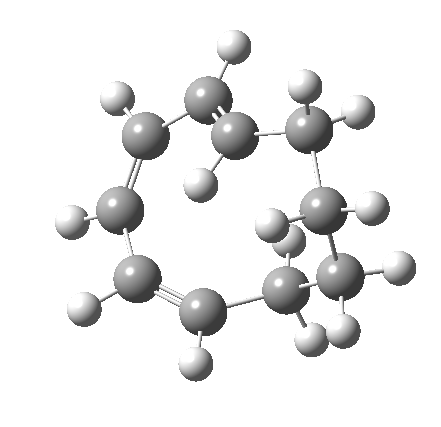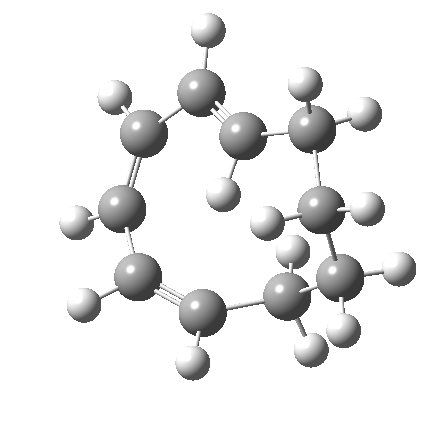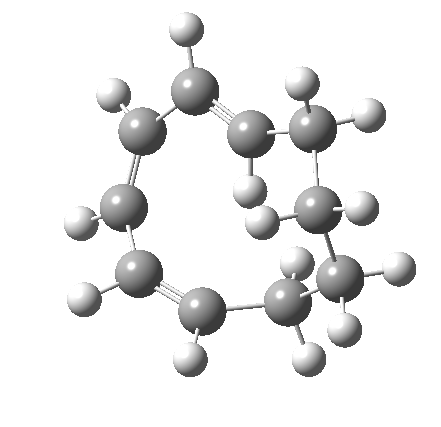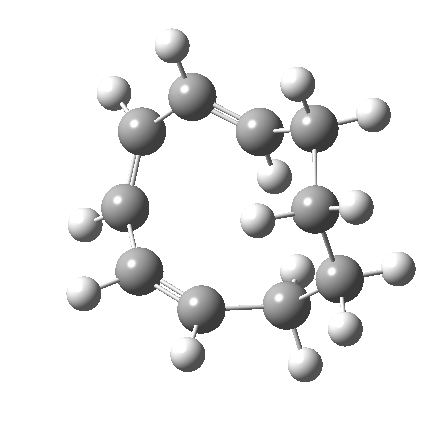 |
|
| 9 ↠ 7 | |
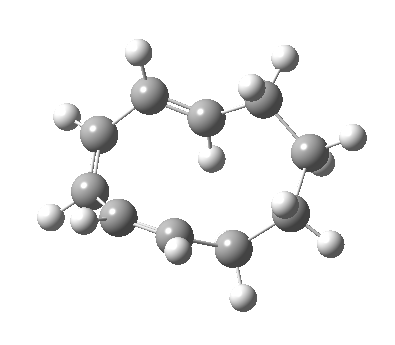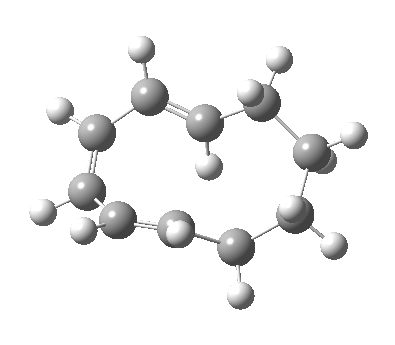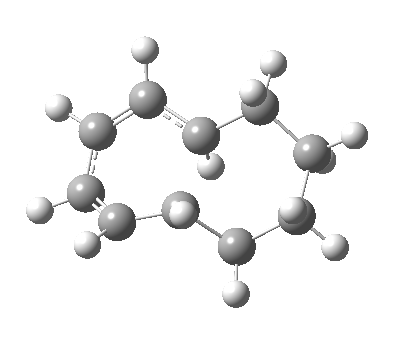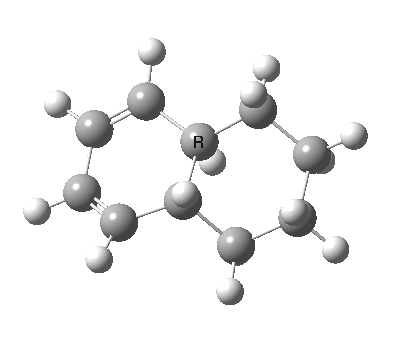 |
|
We can now analyse the two transformations 6 ↠ 8 and 9 ↠ 7. The first involves antarafacial bond formation (blue arrows) at the termini and an accompanying 180° twisting about the magenta bond which creates a second antarafacial component[cite]10.6084/m9.figshare.704841[/cite]. So this is a thermally allowed six-electron (4n+2) electrocyclisation with a double-Möbius twist[cite]10.1039/b510508k[/cite]. The second reaction is a more conventional purely suprafacial version[cite]10.6084/m9.figshare.704995[/cite] (red arrows) of the type Woodward was certainly thinking of; it is 18.0 kcal/mol lower in free energy than the first (the transition state for 6 ↠ 9 is 10.8 kcal/mol lower than that for 9 ↠ 7).
I hope that this detailed exploration of what seems like a pretty simple example at first sight shows how applying a “reality-check” of computational quantum mechanics can cast (some unexpected?) new light on an old problem. We may of course speculate on how to inhibit the pathway 6 ↠ 9 ↠ 7 to allow only 6 ↠ 8 to proceed (the reverse barrier from 8 is quite low, so 8 would have to be trapped at very low temperatures).
Tags: electrocyclic, energy, final product, free energy, Gerhard Fonken, Historical, Niels Bohr, pericyclic, professor, Reaction Mechanism, Robert Woodward, Woodward
Hi Professor,
Some questions not involving Woodward.
Have you ever run some calculations about isocyanide compound?
I’m confused with isocyanide’s role in two Named Reactions, Van Leusen and Ugi FCR.
In Van Leusen, it acts as an electrophile: however, in Ugi, it acts as a nucloephile.
Is isocyanide a carbene-like compound? BTW, the mechanism of Van Leusen is quite complex and obscure.
Please take a look if you have time.
I looked up the Van Leusen reaction in the usual source (is it the one you looked up?), finding a serious error there in the mechanistic diagram. TosMIC is tosyl methyl isocyanide, TsCH2NC, but the Wiki entry on this reaction shows it as TSCH2CN. This does not help in understanding what is going on.
Wiki is one of my usual sources, it indeed gives wrong structure about TosMIC this time. Below are other sources for Van-Leusen and Ugi reactions.
http://www.organic-chemistry.org/namedreactions/van-leusen-reaction.sham
http://www.organic-chemistry.org/namedreactions/ugi-reaction.shtm
I also use “Strategic Applications of Named Reactions in Organic Synthesis” as my mechanism check book. Three sources have three different descriptions of isocyanides: -C=N-R, :C=NCH2Tos -C@N+-R(@ triple bond).Also the different mechanism for Ugi.
Gerhard Fonken was a student of Dauben’s. He graduated from UC Berkeley in 1958, then became a professor and Provost at the University of Texas in Austin.
Fonken was the student who initiated Dauben’s decades long studies in photochemistry with the 1957 publication of “The Structure of
Photoisopyrocalciferol”. More on Dauben here in a biography by Streitweiser: http://www.nasonline.org/publications/biographical-memoirs/memoir-pdfs/dauben-william.pdf
Fonkenmayhave reported this work in his dissertation with Dauben, but you would have to go to Berkeley and get the hard copy.