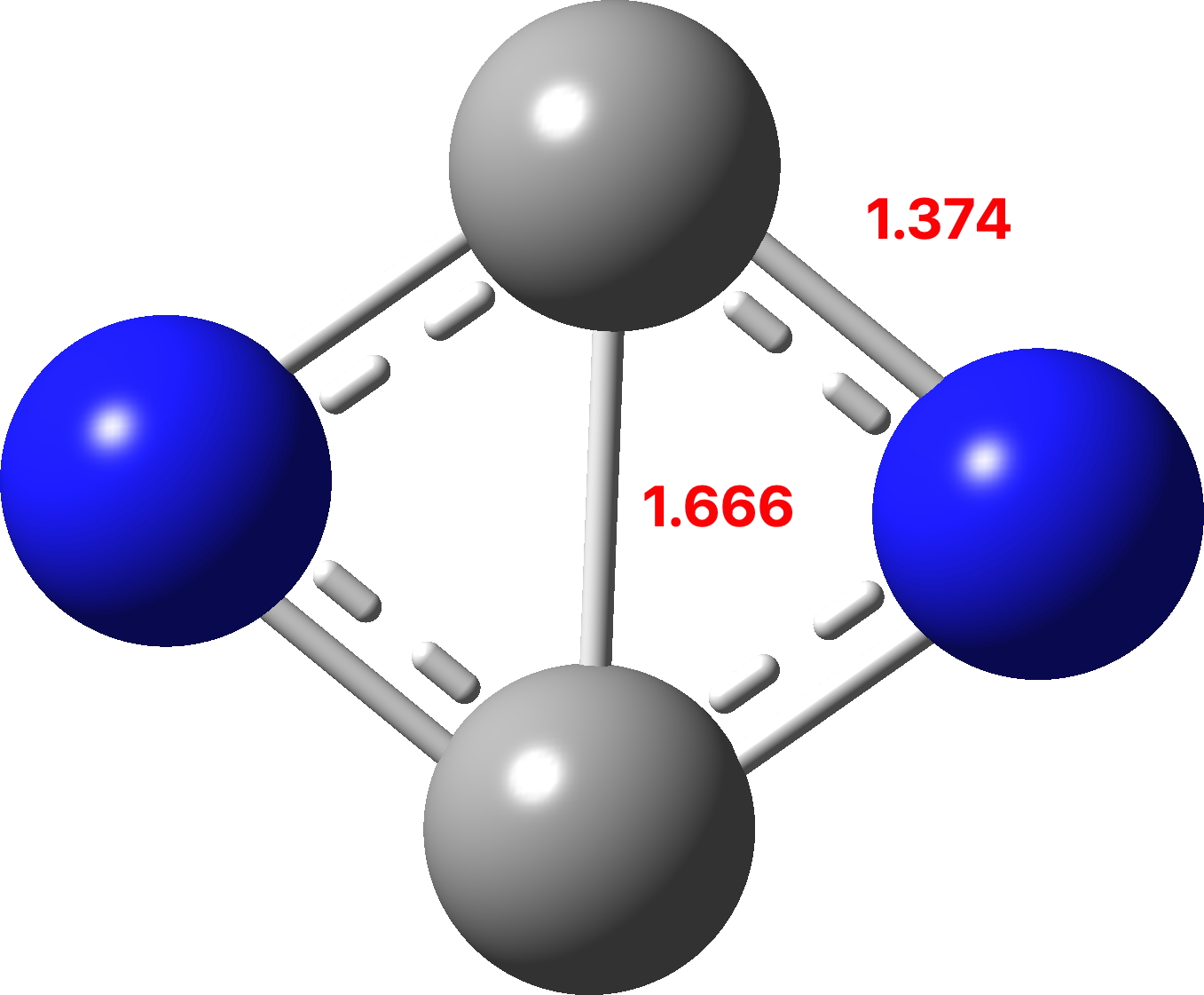
The previous examples of four atom systems displaying two layers of aromaticity illustrated how 4 (B4), 8 (C4) and 12 (N4) valence electrons were partitioned into 4n+2 manifolds (respectively 2+2, 6+2 and 6+6). The triplet state molecule B2C2 with 6 electrons partitioned into 2π and 4σ electrons, with the latter following Baird’s aromaticity rule.[cite]10.1021/ja00769a025[/cite],[cite]10.1021/cr300471v[/cite]. Now for the final missing entry; as a triplet C2N2 has 10 electrons, which now partition into 4 + 6. But would that be 4π + 6σ or 4σ + 6π? Well, in a way neither! Read on.
| Bonding MOs for C2N2. Click image to load 3D model |
|
|---|---|
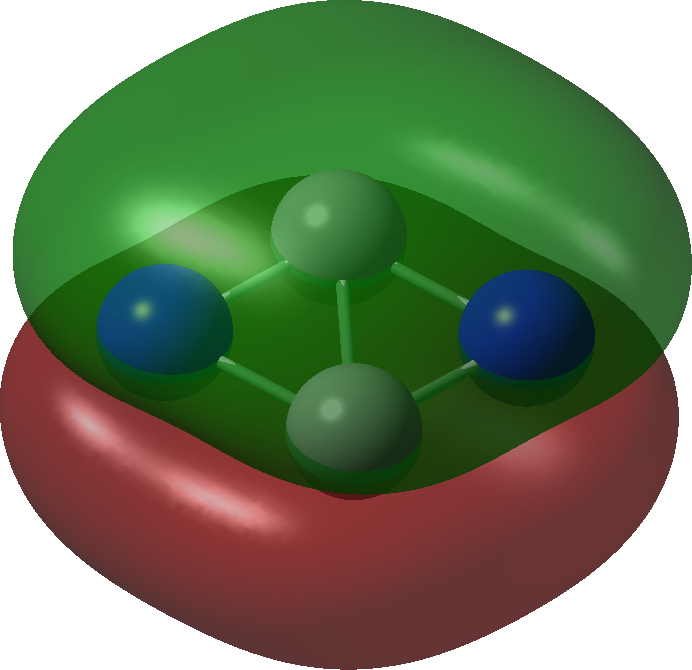
| π3, 1 electron | π2, 1 electron |
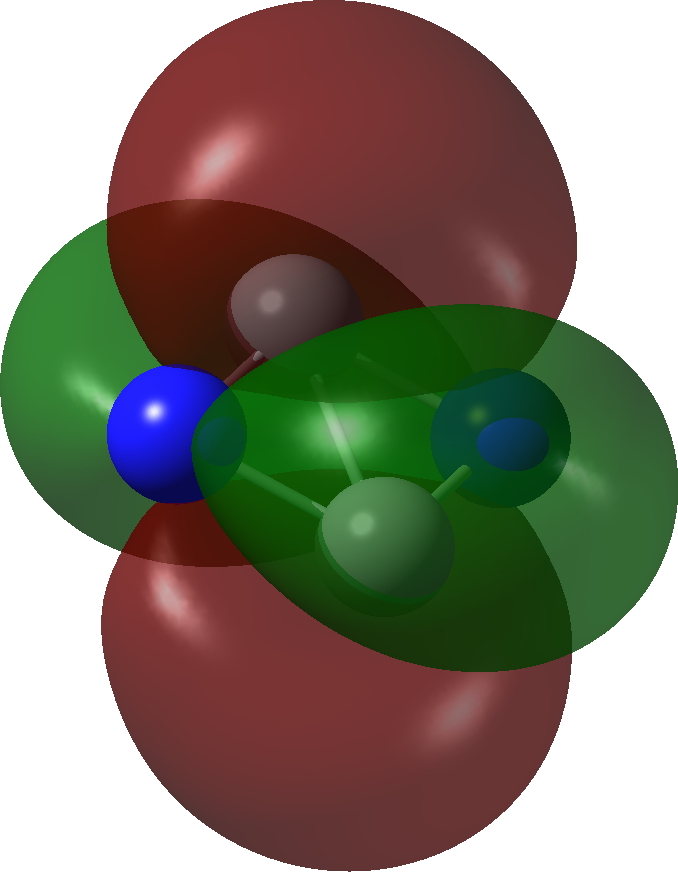 |
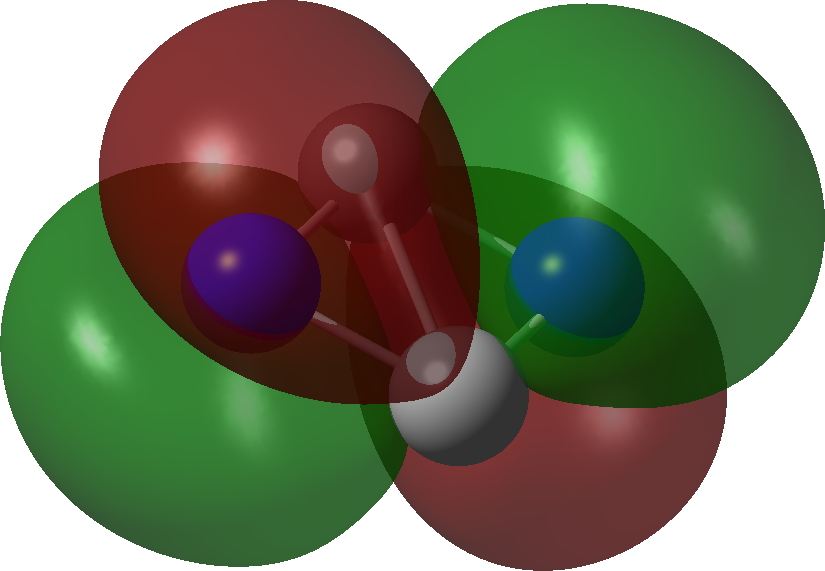 |
| σ3 2 electron | σ2, 2 electron |
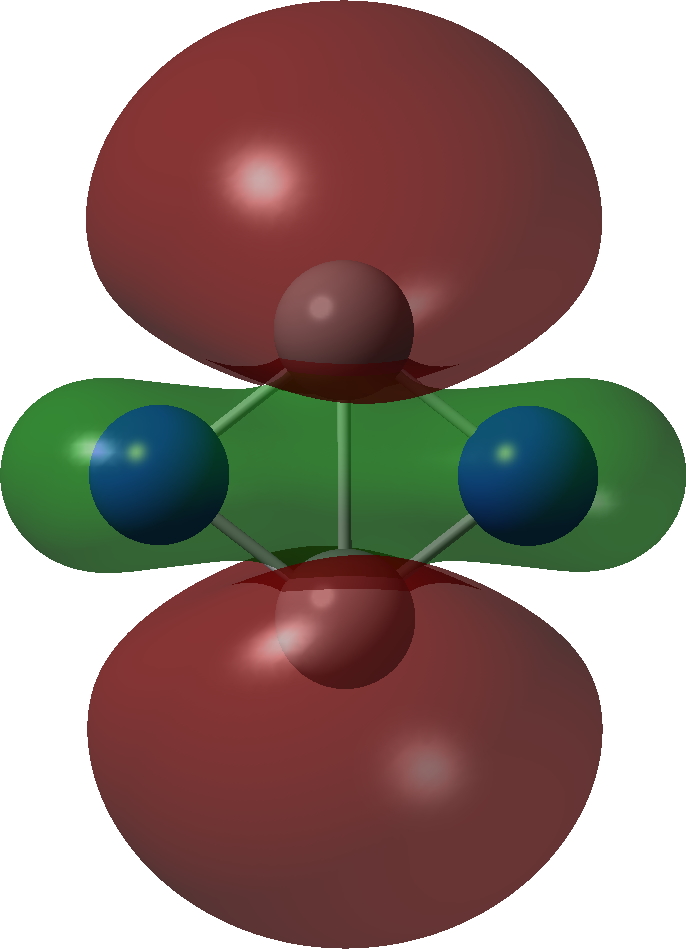 |
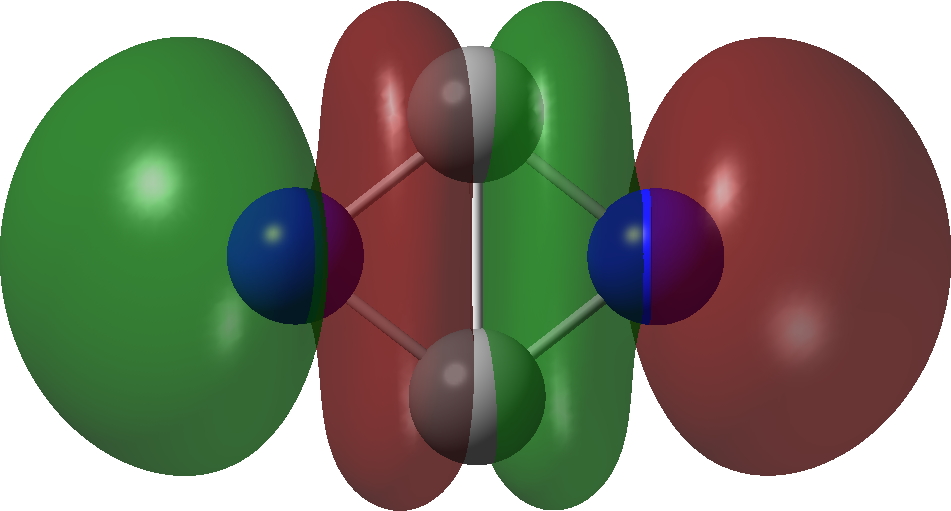 |
| π1 2 electron | σ1, 2 electron |
 |
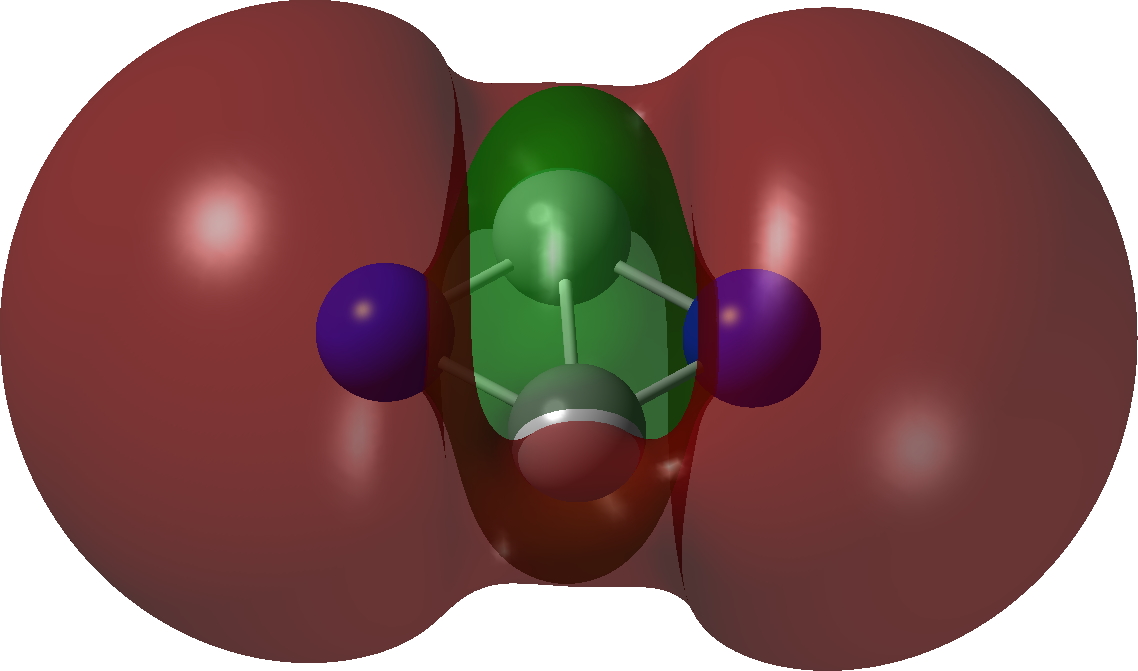 |
The calculations (ωB97XD/Def2-TZVPP and CCSD(T)/Def2-TZVPP) are collected at FAIR DOI: 10.14469/hpc/10346. These show a partitioning into 5σ + 5π, a species that is not a minimum but undergoes a non-planar distortion.
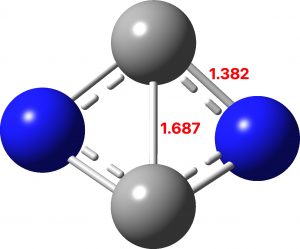
However, the first excited state (the triplet) IS planar and is only 12.5 kcal/mol above the planar 5+5 precursor. It is now partitioned into 6σ and 4π, with the latter conforming to Baird’s rule for open shell triplets.[cite]10.1021/ja00769a025[/cite],[cite]10.1021/cr300471v[/cite] So this is unlike C2B2, which showed 2π + 4σ partitioning with the σ series following Baird’s rule. Now we have two examples in which one of the σ or the π-manifolds follow Baird’s rule and the other follows Hückel’s rule. The systems themselves are somewhat contrived, but they show the simple fun and games that can be had with these aromaticity rules.
This post has DOI: 10.14469/hpc/10350