I have blogged before about the mechanism of this classical oxidation reaction. Here I further explore computed models, and whether they match the observed kinetic isotope effects (KIE) obtained using the natural-abundance method described in the previous post.
There is much previous study of this rearrangement, and the issue can be reduced to deciding whether TS1 or TS2 is rate-limiting. The conventional text-book wisdom is that the carbon migration step TS2 is the “rds” and it was therefore quite a surprise when Singleton and Szymanski[1] obtained KIE which seemed to clearly point instead to TS1 as being rate limiting, inferred from a large 13C effect (~1.05) at the carbonyl carbon (blue star) and none at the α-carbon (red star). This result (for this specific reaction and conditions, which is dichloromethane as solvent) is now routinely quoted[2] when the mechanism is discussed. This latter article reports[2] calculated energetics for TS1 and TS2 (see Table 1 in this article) and after exploring various models, the conclusion is that TS1 and TS2 are essentially isoenergic. However, no isotope effects are computed for their models, and so we do not know if TS1 or TS2 agrees better with the reported values.[2] Since I had managed to get pretty good agreement with experimental KIEs using the ωB97XD/Def2-TZVPP/SCRF=xylenes model for the Diels-Alder reaction, I thought I would try the same method to see how it performs for the Baeyer-Villiger.
It is in fact non-trivial to set up a consistent model. Using arrow pushing, one can on paper draw three variations for TS1, the formation of the peroxyhemiacetal tetrahedral intermediate (TI) and also often called the Criegee intermediate.
- TS1a is the “text-book” variation, involving the production of a zwitterionic intermediate which immediately undergoes a proton transfer (PT). The arrows tend not to be used for this last step, since the direct transfer would involve a 4-membered ring and a highly non-linear geometry at the transferring proton which is understood to be “unfavourable”. Such zwitterions involve a large degree of charge separation and hence a large dipole moment. In a non-protic solvent such as dichloromethane, one is very loath to use such species in a mechanism, and it’s not modelled here either.
- Using just cyclohexanone and peracid, it is in fact difficult to avoid ionic species. TS1b is an attempt which shows the proton transfer is done first on the peracid to create a so-called carbonyl ylid, and this then reacts with the ketone
- If however a proton transfer agent is introduced as TS1c, one can use this species (shown in red above) to transfer the proton as part of a concerted mechanism; this was in fact the expedient used in the earlier theoretical study[2] and this route tends to avoid much if not all of the charge separation. The acid comes from the product of the reaction, and hence the kinetics may in fact have an induction period when this acid builds up. The initial proton transfer reagent may also be traces of water present in reagents or solvent. Singleton and Szymanski in fact include no supporting information in their article and so we do not know what the concentrations used were (assumed for the present discussion as 1M) whether everything was rigorously dried, or indeed what the kinetic order in [peracid] turned out to be.
The same problem is faced with TS2; how to transfer a proton? Because we want to compare the relative energies of TS1 and TS2, we also have to atom-balance the mechanism, and so the additional acid component introduced into TS1c is also retained in two alternative mechanisms for TS2 (and for TS1b).
- TS2a uses just the components of the tetrahedral intermediate (TI), but again in a fashion that requires no charge separation during the reaction. The additional acid component (red) plays a passive role, hydrogen bonding to the TI.
- TS2b now incorporates the additional acid by expanding the ring (green) in an active role.
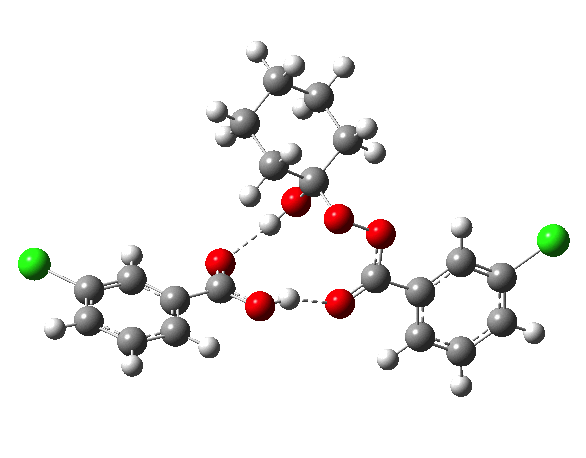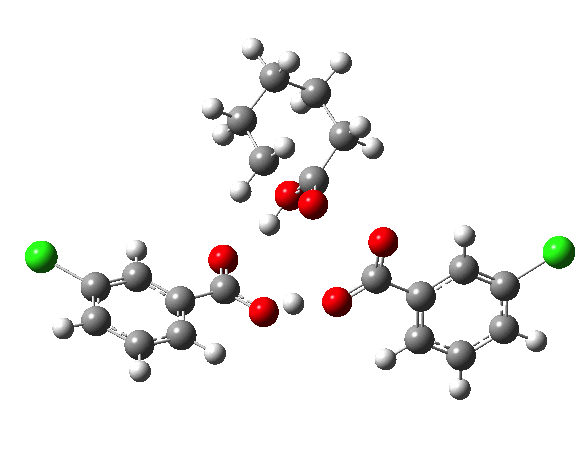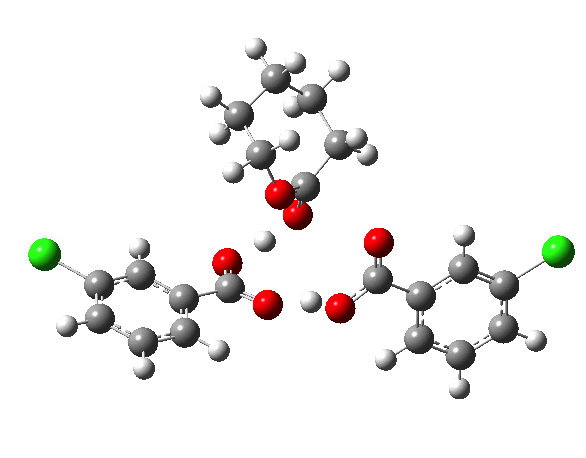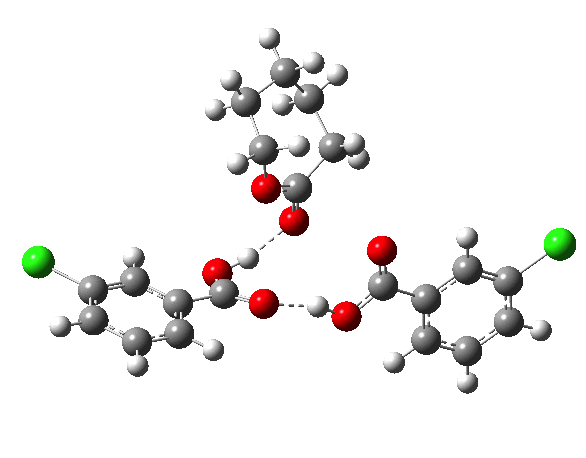
IRCs using the 6-311G(d,p) basis) for TS1[3] and TS2[4] are interesting in revealing relative synchronicity of the proton transfers for TS1 but asynchronicity for TS2 involving a hidden intermediate.
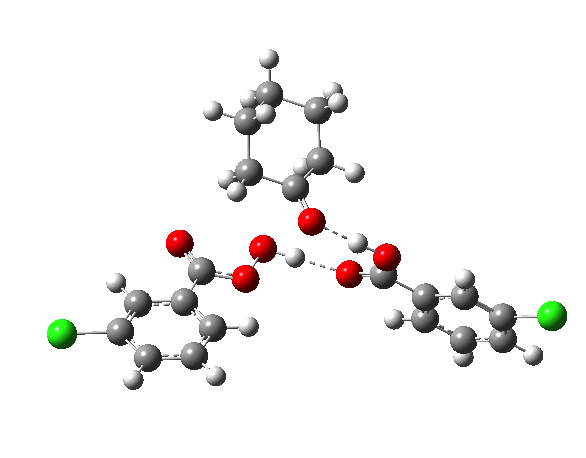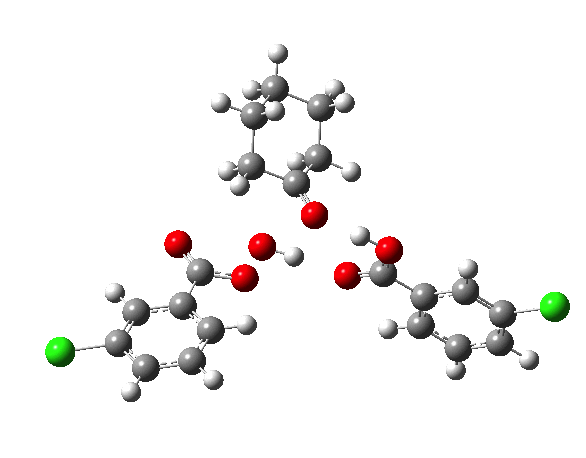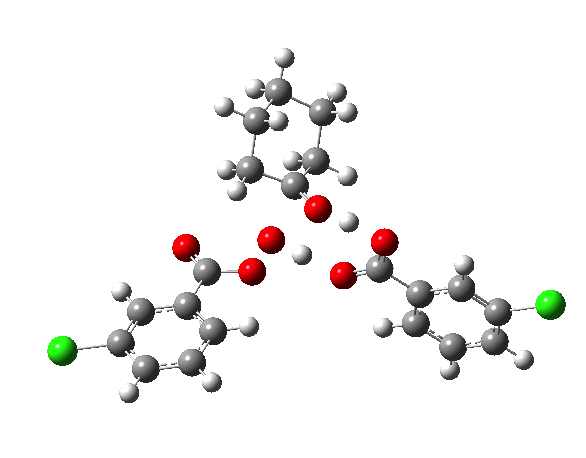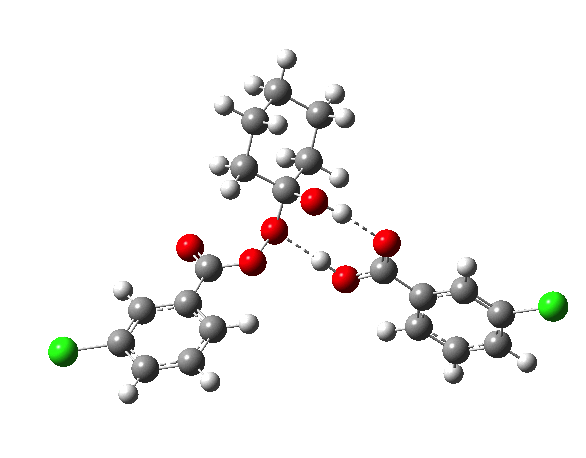
The energy, energy gradient and dipole moment magnitudes for this second step are particularly fascinating. The dipole moment starts off quite small (3.1D) at the TI, and is still so at the TS, but almost immediately afterwards, it shoots up to ~12D as the hidden intermediate develops (IRC ~4) Two successive proton transfers (IRC ~6, 7) then reduce the value down again.
A table of results can now be constructed for these various models, evaluating two different basis sets for the calculation.
| system | ΔΔG298 (1M) ωB97XD/6-311G(d,p)/SCRF=DCM, kcal/mol |
Dipolemoment,D | ΔG298 (1M) ωB97XD/Def2-TZVPP/SCRF=DCM |
|---|---|---|---|
| Reactants | +1.4a | – | -3.3a[5],[6],[7] |
| Complexed state | 0.0[8] | 5.0 | 0.0[9] |
| TS1a | n/a | n/a | n/a |
| TS1b | 32.9[10] | 8.6 | 32.2[11] |
| TS1c | 14.9[12] | 3.0 | 16.1[13] |
| TI | -1.7[14] | 3.1 | -0.3[15] |
| TS2a | 22.2[16] | 9.3 | 25.0[17] |
| TS2b | 20.2[12] | 5.4 | 22.7[18] |
| Product | -69.8[19] | 5.3 | [20] |
aThis value is corrected to a standard state of 1M for a termolecular reaction by 3.78 kcal/mol from the computed free energies at 1 atm as described previously.[21]
- Firstly, one must note that the resting state for the reactants depends on the concentration. At 1M at the higher basis set, its the separated reactants, but at the lower it is the hydrogen bonded complex between them. Increasing the concentration would favour the latter.
- TS1c is significantly lower in free energy than TS2b, a result somewhat at variance with the earlier report.[2] The functional used in the present calculation, the basis set, the dispersion model and the solvation model are all improvements on the original work.
- Likewise, the energy of TI, the Criegee intermediate emerges as similar to the reactants. Coupled with the magnitude of the barrier for TS1c this does tend to point to a relatively rapid pre-equilibrium and that TS2b determines the rate of reaction.
Kinetic isotope effects for our models
Having constructed models, we can now subject them to testing against the measured kinetic isotope effects.[1]
- The measured values are shown above. The first set (a) are what are described as intermolecular isotope effects and result from measuring changes in the isotopic abundance obtained by recovering unreacted starting material after a large proportion of the reaction has gone to completion. This was interpreted as indicating TS1 was rate limiting. Using instead the uncomplexed cyclohexanone has only a small effect (C1: 1.023 complexed, 1.021 uncomplexed).
- The values in parentheses were obtained using the TS1c model above and are relative to the complexed reactant involving hydrogen bonds between the cyclohexanone, the peracid and the acid catalyst. The agreement can only be described as partial.
- The predicted 13C isotope effect at C1 is about half of the measured value. The previous calibration of the method being used had resulted in agreement within experimental error for the Diels Alder reaction, and so this large disagreement is unexpected.
- The 2H KIE at C2 is within experimental error.
- The 2H KIE at C3 is badly out. Here, it is the experimental result that seems wrong, since there is no reason to expect any KIE at this position especially since the 13C at the same position is 1.00 for both measured and calculated values.
- So we might infer an inconclusive result. I can only speculate on the computed model here, and invoke in effect the variation principle. If the model is wrong, we would expect a more correct model to have a lower rather than higher energy relative to reactants. The free energy of activation however is already low, corresponding to a very fast room temperature reaction; too fast indeed to easily recover any unreacted starting material if that were to be rate limiting!
- Set (b) corresponds to what is described as an intramolecular KIE as defined by TS2, since it is measured from isotopic ratio changes in the product rather than reactant as the reaction progresses.
- The value in (…) is relative to the complexed reactants and the value in […] is relative to TI.
- The predicted 13C isotope effect at C2m (the migrating carbon) agrees within experimental error with the measured value if the TI is used as the reference. This nicely shows how isotope effects for what may not be a rate limiting step can be measured by this technique.
- The predicted 13C isotope effect at C1 (which is not reported in the original article) relative to TI is significant, and it would be nice to confirm the computed model by a measurement at this position.
- The other KIE also agree reasonably with experiment when TI is specified as the reactant for this step.
So is there support from the calculations for the formation of the semi-peroxyacetal being rate limiting, as claimed by Singleton and Szymanski[1]? There is no doubt that the KIE obtained from measuring the product is different from measuring the reactant, but the lack of agreement for two of the measured values for TS1 is a concern. Perhaps one might conclude that this is an experiment well worth repeating. Of the two computed models, TS1 and TS2, the variation principle would again lead us to suspecting that the one with higher energy can only be decreased by improvement, whereas improvement of the one with the lower energy cannot also increase its relative energy. So if a new model for the carbon migration step can be found, its activation free energy must be lower than that already identified. But the excellent agreement between TS2b shown in (b) suggests that this model is already pretty good! Lowering its energy by >7kcal/mol to make TS1 rate limiting would probably require quite a different model.
What I think is more certain is the value of subjecting the measured KIE to computed models, in the knowledge that if the model is indeed realistic a good agreement should be expected. And it is a shame that the natural abundance KIE method cannot be applied to oxygen isotope effects, which would surely settle the issue.‡ And I should end by reminding that there is evidence that the mechanism may be quite sensitive to variation of solvent, ketone, peracid, pH, etc, and so these conclusions only apply to this specific reaction in dichloromethane.
‡ For TI > TS2, the 18O KIE is predicted as 1.048 (peroxy oxygen) and 1.032 (acyl oxygen). For Reactant > TS1, the values are respectively 0.998 and 1.003.
References
- D.A. Singleton, and M.J. Szymanski, "Simultaneous Determination of Intermolecular and Intramolecular 13C and 2H Kinetic Isotope Effects at Natural Abundance", Journal of the American Chemical Society, vol. 121, pp. 9455-9456, 1999. http://dx.doi.org/10.1021/ja992016z
- J.R. Alvarez-Idaboy, and L. Reyes, "Reinvestigating the Role of Multiple Hydrogen Transfers in Baeyer−Villiger Reactions", The Journal of Organic Chemistry, vol. 72, pp. 6580-6583, 2007. http://dx.doi.org/10.1021/jo070956t
- Henry S Rzepa., "C20H20Cl2O6", 2015. http://dx.doi.org/10.14469/ch/191318
- Henry S Rzepa., "C20H20Cl2O6", 2015. http://dx.doi.org/10.14469/ch/191317
- Henry S Rzepa., "C 7 H 5 Cl 1 O 2", 2015. http://dx.doi.org/10.14469/ch/191322
- Henry S Rzepa., "C 7 H 5 Cl 1 O 3", 2015. http://dx.doi.org/10.14469/ch/191323
- Henry S Rzepa., "C 6 H 10 O 1", 2015. http://dx.doi.org/10.14469/ch/191324
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191307
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191315
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191313
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191325
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191306
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191312
- Henry S Rzepa., "C20H20Cl2O6", 2015. http://dx.doi.org/10.14469/ch/191311
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191319
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191314
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191321
- Henry S Rzepa., and Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191320
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191310
- Henry S Rzepa., "C 20 H 20 Cl 2 O 6", 2015. http://dx.doi.org/10.14469/ch/191327
- J.R. Alvarez-Idaboy, L. Reyes, and J. Cruz, "A New Specific Mechanism for the Acid Catalysis of the Addition Step in the Baeyer−Villiger Rearrangement", Organic Letters, vol. 8, pp. 1763-1765, 2006. http://dx.doi.org/10.1021/ol060261z
Tags: ATM, Baeyer–Villiger oxidation, Chemistry, Dipole, energy, energy gradient, Kinetic isotope effect, Physical organic chemistry
If you look at the old Fry KIEs, it is pretty clear that the rate-limiting step changes with reactants. I would not have called our results surprising. The focus of the communication was the KIE method, not the mechanism.
I should note that oxygen isotope effects can be measured at natural abundance. We did this with Claisen rearrangements and with TMSCl-catalyzed cuprate conjugate additions. It is a tricky experiment, due to the line widths. I vaguely remember us trying this with the Baeyer-Villiger, but I would have to look through notebooks to make sure, and if we tried it, it must not have worked.
At the time (1999), SI was less common (and a communication was still mostly a communication). Today we would probably give you 200 pages for the same work.
I would have to look up the details, but I suspect that the reaction was carried out with 60% mCPBA under high-concentration heterogeneous reaction conditions. Our wont at the time was to study reactions under typical synthetic conditions, as opposed to “mechanistic conditions”, and we had done this with other reactions such as bromination of alkenes and cuprate conjugate additions. Under mechanistic conditions, everything is purified, there is a clean, well-behaved rate law, one knows all the molecules involved, and the concentrations are usually dilute. Some reactions are rather difficult to perform under mechanistic conditions, the bromination of alkenes being one. Under synthetic conditions, you pull the materials off the shelf and do the reaction in a way that works easily and well. With a polar reaction in solution, with O-O bonds breaking, with proton transfers, and with non-mechanistic experimental conditions, caveat calculator.
Thanks Dan for your insights!
I agree your focus was on the KIE method. Unless I have missed it, your ground breaking analysis of two species such as reactant and product still remains quite uncommon, which is a shame.
Re oxygen isotope effects, its good to know that the difficulties of 18O NMR do not prevent all measurements.
Re SI, I agree that in 1999 it was uncommon but also that perhaps 100-200 pages has now gone to the other extreme. My take is that we should now be focussing not so much on quantity but on quality of SI, or RDM (research data management) as the modern parlance has it. Another acronym summarises this more nicely: FAIR (findable, accessible, interoperable, re-usable). Many of my posts here address this issue, and in the UK at least the funding councils are getting more and more prescriptive about how the data for a funded project should be managed. I am sure you will agree that pouring all the data into one 200 page PDF document is not necessarily good management. As an experiment in such RDM, my post included a number of “dataDOIs”, and my reason is that these allow access to the force constant matrix for each model, and hence allow any interested party to compute whatever isotopic combinations they wish. That would not be possible using conventional SI, which would indeed balloon beyond 200 pages if the Hessian matrices were to be included. We have an article in J Cheminformatics coming out shortly (do: 10.1186/s13321-015-0081-7 which goes into some of the technical details of how we did this in what we hope is an “end-user friendly” manner.
Yrs, if the reaction was heterogenous, that makes modelling even more of a challenge, and in particular in determining what the kinetic order in peracid is.
May I ask one question which I pondered whilst writing the blog? Suppose the formation of the hemi-peroxyacetal (the TI) was exo-energic and fast (the calculations at the Def2-TZVPP basis level show it slightly endo-energic), then you have fast formation of a common intermediate (the “resting state”), the output channels of which are either the lactone or the ketone. Measuring isotopic abundance changes in ketone or lactone should then reveal the KIEs out of this channel. I did compute the KIE using the TI as the reference point for TS1 to see if they led to better agreement with your reported values for TS1. They did not.
Many moons ago, we looked at stable tetrahedral intermediates which could easily be detected by NMR or forced to form by application of pressure. Perhaps Ac-SSH “peracids” might form these? At any rate, do we know for certain whether the “resting state” in your reaction is ketone or the tetrahedral intermediate? Or does it matter if the two were to be in fast equilibrium in terms of the KIE analysis? I appreciate that your results indicate TS1 as a rate-limiting irreversible process, but we do know that many such Tis are formed both quickly and reversibly.
Thanks Dan for your insights!
I agree the focus was on the KIE method. Unless I have missed it, your ground breaking analysis of two species such as reactant and product still remains quite uncommon, which is a shame.
Re oxygen isotope effects, its good to know that the difficulties of 18O NMR do not prevent all measurements.
Re SI, I agree that in 1999 it was uncommon but also that perhaps 100-200 pages has now gone to the other extreme. My take is that we should now be focussing not so much on quantity but on quality of SI, or RDM (research data management as the modern parlance has it). Many of my posts here address this issue, and in the UK at least the funding councils are getting more and more prescriptive about how the data for a funded project should be managed. I am sure you will agree that pouring all the data into a 200 page PDF document is not necessarily good management. As an experiment in such RDM, my post included a number of “dataDOIs”, and my reason is that these allow access to the force constant matrix for each model, and hence allow any interested party to compute whatever isotopic combinations they wish. That would not be possible using conventional SI, which would indeed balloon beyond 200 pages if the Hessian matrices were to be included. We have an article in J Cheminformatics coming out shortly (do: 10.1186/s13321-015-0081-7 which goes into some of the technical details of how we did this in what we hope is an “end-user friendly” manner.
Yrs, if the reaction was heterogenous, that makes modelling even more of a challenge!
May I ask one question which I pondered whilst writing the blog? Suppose the formation of the hemi-peroxyacetal (the TI) was exo-energic and fast (the calculations at the Def2-TZVPP basis level show it slightly endo-energic), then you have fast formation of a common intermediate, the output channels of which are either the lactone or the ketone. Measuring isotopic abundance changes in ketone or lactone should then reveal the KIEs out of this channel. I did compute the KIE using the TI as the reference point for TS1 to see if they led to better agreement with your reported values for TS1. They did not.
Many moons ago, we looked atstable tetrahedral intermediates which could easily be detected by NMR (or forced to form by application of pressure). Perhaps Ac-SSH “peracids” might form these? At any rate, do we know for certain whether the “resting state” in your reaction is ketone or the tetrahedral intermediate? Or does it matter if the two were to be in fast equilibrium in terms of the KIE analysis? We do know that many Tis are indeed formed both quickly and reversibly.
Just a note – there is no 18O NMR. There is 17O NMR.
To address your question, I will use = for rapid equilibria and -> for an irreversible conversion. A will be my starting material and B will be either a reagent or a catalyst. I will be referring to the case where the KIES are competition KIEs (A is a mixture of isotopomers), not absolute rate constants (which at times can be a different story).
For
A + B = C -> TS‡ -> product
There is no ambiguity when C has a higher free energy than A + B; the isotope effect reflects TS versus A.
People get confused however when C is lower in free energy than A + B. (I will just deal with the case where C is much more stable than A + B). The answer becomes “it depends” but most often the isotope effect still reflects TS versus A, not C.
When B is a catalyst (present in small amounts relative to A) then the isotopic composition of C represents the equilibrium IE for formation of C and the overall KIE is the multiple of the equilibrium IE for the first step times the KIE for the second step, which equals the KIE if calculated with A as the starting material.
It is more complicated when B is a stoichiometric reagent.
When B is added slowly and reacts as it is added, the effect is the same as when it is a catalyst.
When B is present in excess so that all A has become C, then A is irrelevant and the KIE reflects TS vs C.
When A exceeds B, say by 1 to 0.8, the math is much more complicated. Early in the reaction, C exceeds A and its isotopic composition does not fully reflect the equilibrium isotope effect, so the acting KIE is closer to TS versus C than TS versus A. As the reaction proceeds, the relative amount of A versus C increases and the acting KIE moves toward that for TS versus A. The later stages of the reaction have a relatively bigger effect on the overall observed KIE (measured on recovered A), so the final observation is still closer to TS versus A than TS versus C. This is true no matter how much more stable C is than A+B.
A bit of mathematical modeling on and Excel spreadsheet handles any situation.
The qualitative rule I teach is that the starting material for calculations is what is actually there in the reaction flask.
I should mention that for intramolecular KIEs measured on the product, the choice of formal starting material is irrelevant.